
 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 首先利用全等三角形的判定方法利用SAS证明△BAF≌△ADE,即可得出AE=BF,进而得出∠BFA+∠EAD=90°,即AE⊥BF,利用三角形全等即面积相等,都减去公共面积剩余部分仍然相等,即可得出D正确,过点E作EG⊥AB交BF与点H.然后依据直角三角形中斜边大于任何一条直角边进行判断即可.
解答 解:∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,
∴AF=DE.
在△ABF和△DAE中,$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠ADE}\\{AF=DE}\end{array}\right.$,
∴△ABF≌△DAE.
∴AE=BF,故(1)正确.
∵△ABF≌△DAE,
∴∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,即AE⊥BF,故(2)正确.
∵△ABF≌△DAE,
∴S△ABF=S△ADE.
∴S△AOB=S△ABF-S△AOF,S四边形DEOF=S△ADE-S△AOF,即∴S△AOB=S四边形DEOF.
如图所示:过点E作EG⊥AB,则EG=AD.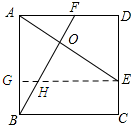
∵HE>OE,GE>HE,
∴GE>OE.
∴AD>OE,故(3)错误.
故选:B.
点评 此题主要考查了正方形的性质以及全等三角形的判定与性质和反证法的应用等知识,得出△BAF≌△ADE,从而得出相应等量关系是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | $\sqrt{{a^2}-{b^2}}$=a-b | C. | $\frac{\sqrt{6}+\sqrt{8}}{2}$=$\sqrt{3}$+$\sqrt{4}$=$\sqrt{3}$+2 | D. | a$\sqrt{x}$-b$\sqrt{x}$=(a-b)$\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y=y2 | C. | y1<y2 | D. | 不能比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
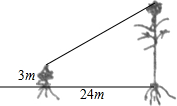 有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m远的一棵大树上,大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?(画出符合题意的几何图形,并求解)
有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m远的一棵大树上,大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?(画出符合题意的几何图形,并求解)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1的度数为( )
如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1的度数为( )| A. | $\frac{70}{{2}^{n}}$ | B. | $\frac{70}{{2}^{n+1}}$ | C. | $\frac{70}{{2}^{n-1}}$ | D. | $\frac{70}{{2}^{n+2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com