
 一队学生从学校出发去劳动基地军训,行进的路程与时间的图象如图所示,队伍走了0.9小时后,队伍中的通讯员按原路加快速度返回学校拿材料,通讯员经过0.5小时后回到学校,然后随即按原来加快的速度追赶队伍,恰好在劳动基地追上学生队伍.设学生队伍与学校的距离为d1,通讯员与学校的距离为d2,试根据图象解决下列问题:
一队学生从学校出发去劳动基地军训,行进的路程与时间的图象如图所示,队伍走了0.9小时后,队伍中的通讯员按原路加快速度返回学校拿材料,通讯员经过0.5小时后回到学校,然后随即按原来加快的速度追赶队伍,恰好在劳动基地追上学生队伍.设学生队伍与学校的距离为d1,通讯员与学校的距离为d2,试根据图象解决下列问题:分析 (1)根据函数图象可得:当t=0.9h时,学生队伍走的路程s=4.5km,即可解答;
(2)通讯员经过0.5小时后回到学校,0.9+0.5=1.4,所以B点的坐标为(1.4,0),当0.9≤t≤3.15时,分别求线段AB和线段BC的解析式,即可解答;
(3)求出线段OC的解析式,分两种情况进行讨论即可解答.
解答 解:(1)根据函数图象可得:当t=0.9h时,学生队伍走的路程s=4.5km,
∴学生队伍行进的速度为:4.5÷0.9=5(km/h),
故答案为:5.
(2)∵通讯员经过0.5小时后回到学校,0.9+0.5=1.4,∴B点的坐标为(1.4,0)
设线段AB的解析式为:d2=kt+b(k≠0),(0.9≤t≤1.4),
又过点A(0.9,4.5)、B(1.4,0),
∴$\left\{\begin{array}{l}{0.9k+b=4.5}\\{1.4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-9}\\{b=12.6}\end{array}\right.$,
∴线段AB的解析式为:d2=-9t+12.6,(0.9≤t≤1.4).
∵通讯员按原来的速度随即追赶队伍,∴速度为4.5÷0.5=9千米/小时.
设线段BC的解析式为:d2=9t+m,(1.4≤t≤3.15),
又过点B(1.4,0),
∴0=9×1.4+m,
解得:m=-12.6,
∴线段BC的解析式为:d2=9t-12.6,(1.4≤t≤3.15),
∴${d}_{2}=\left\{\begin{array}{l}{-9t+12.6(0.9≤t≤1.4)}\\{9t-12.6(1.4<t≤3.15)}\end{array}\right.$.
(3)设线段OC的解析式为:d1=nt(n≠0),又过点A(0.9,4.5),
∴4.5N=0.9,
∴n=5.
∴线段OC的解析式为:d1=5t,
设时间为t小时,学生队伍与通讯员相距不超过3千米,下面分两种情况讨论:
①当0.9≤t≤1.4时,d1-d2≤3,即5t-(-9t+12.6)≤3,
解得:$t≤\frac{39}{35}$,
∴$0.9<t≤\frac{39}{35}$.
②当1.4≤t≤3.15时,d1-d2≤3即5t-(9t-12.6)≤3,
解得:t≥2.4,
∴2.4≤t≤3.15.
故通讯员离开队伍后他们能用无线对讲机保持联系时t的取值范围为$0.9<t≤\frac{39}{35}$
或2.4≤t≤3.15.
点评 本题考查了一次函数的应用,解决本题的关键是分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
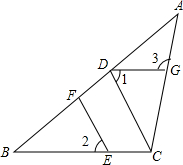 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.27×105 | B. | 27×103 | C. | 2.7×103 | D. | 2.7×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限或第三象限 | B. | 第一象限或第二象限 | ||
| C. | 第二象限或第四象限 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
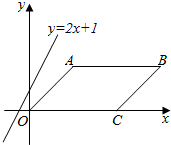 秒1个单位的速度向右平移,经过3秒该直线可将?OABC的面积平分.
秒1个单位的速度向右平移,经过3秒该直线可将?OABC的面积平分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com