
【题目】已知正比例函数y=k1x的图象与反比例函数y=![]() 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
【答案】(1)正比例函数y=![]() x;反比例函数y=
x;反比例函数y=![]() ;(2)见解析;(3)x<﹣2或0<x<2.
;(2)见解析;(3)x<﹣2或0<x<2.
【解析】
试题分析:(1)根据待定系数法,可得函数解析式;
(2)根据函数解析式确定出图象所经过的点的坐标,再画出图象即可.
(3)根据图象和交点坐标即可求得.
解:(1)由正比例函数y=k1x的图象与反比例函数y=![]() 的图象的一个交点是(2,3),得
的图象的一个交点是(2,3),得
3=2k1,3=![]() .
.
解得k1=![]() ,k2=6.
,k2=6.
正比例函数y=![]() x;反比例函数y=
x;反比例函数y=![]() ;
;
(2)画出函数的图象如图:
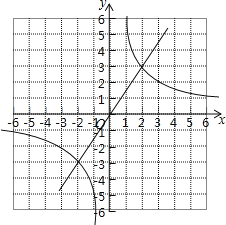
两个函数图象的一个交点的坐标(2,3),猜想另一个交点的坐标(﹣2,﹣3),
把(﹣2,﹣3)代入y=![]() 成立;
成立;
(3)由图象可知:比例函数值大于正比例函数值的x的取值范围是x<﹣2或0<x<2.


科目:初中数学 来源: 题型:
【题目】已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成( )
A.10b+a
B.ba
C.100b+a
D.b+10a
查看答案和解析>>
科目:初中数学 来源: 题型:
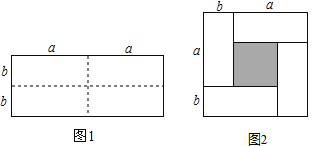
【题目】如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(a﹣b)2,(a+b)2,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
(3)已知a+b=4,ab=3.求代数式a﹣b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com