
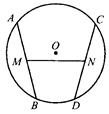
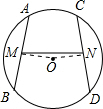
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
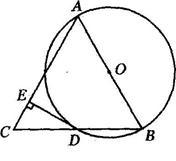
 弧AE=弧BE ; ④2CE·AB=BC2,
弧AE=弧BE ; ④2CE·AB=BC2,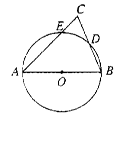
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
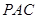 圆
圆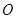 的内接正三角形,那么∠
的内接正三角形,那么∠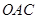 ﹦ ;
﹦ ;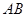 是圆
是圆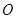 的直径,
的直径,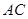 是圆的任意一条弦,∠
是圆的任意一条弦,∠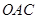 ﹦
﹦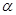 ﹒
﹒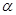 ﹦45°,那么
﹦45°,那么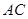 能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒
能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒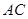 是圆的内接正
是圆的内接正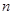 边形的一边,则用含
边形的一边,则用含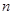 的代数式表示
的代数式表示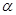 应为 ﹒
应为 ﹒
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
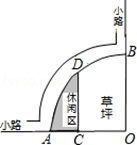
A.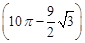 米2 米2 | B.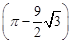 米2 米2 | C.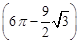 米2 米2 | D.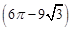 米2 米2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
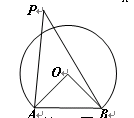
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com