
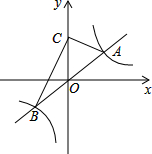
 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=$\frac{3}{4}$x的图象交于A、B两点(点A在第一象限).
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=$\frac{3}{4}$x的图象交于A、B两点(点A在第一象限).分析 (1)①根据点A的横坐标是4,可以求得点A的纵坐标,从而可以求得k的值;
②根据反比例函数的性质,可以写出y的取值范围;
(2)根据点C为y轴正半轴上一点,∠ACB=90°,且△ACB的面积为10,灵活变化,可以求得点A的坐标,从而可以求得k的值.
解答 解:(1)①将x=4代入y=$\frac{3}{4}$x得,y=3,
∴点A(4,3),
∵反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=$\frac{3}{4}$x的图象交于A点,
∴3=$\frac{k}{4}$,
∴k=12;
②∵x=-4时,y=$\frac{12}{-4}$=-3,x=1时,y=$\frac{12}{1}$=12,
∴由反比例函数的性质可知,当-4<x<1(x≠0)时,y的取值范围是y<-3或y>12;
(2)设点A为(a,$\frac{3}{4}a$),
则OA=$\sqrt{{a}^{2}+(\frac{3a}{4})^{2}}$=$\frac{5a}{4}$,
∵点C为y轴正半轴上一点,∠ACB=90°,且△ACB的面积为10,
∴OA=OB=OC=$\frac{5a}{4}$,
∴S△ACB=$\frac{1}{2}×\frac{5a}{4}×2a$=10,
解得,a=$2\sqrt{2}$,
∴点A为(2$\sqrt{2}$,$\frac{3\sqrt{2}}{2}$),
∴$\frac{3\sqrt{2}}{2}$=$\frac{k}{2\sqrt{2}}$,
解得,k=6,
即k的值是6.
点评 本题考查一次函数与反比例函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 监测点 | 荔园 | 西乡 | 华侨城 | 南油 | 盐田 | 龙岗 | 洪湖 | 南澳 | 葵涌 | 梅沙 | 观澜 |
| AQI | 15 | 31 | 25 | 24 | 31 | 24 | 25 | 25 | 34 | 20 | 26 |
| 质量 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 |
| A. | 25,25 | B. | 31,25 | C. | 25,24 | D. | 31,24 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.36×108 | B. | 2.36×109 | C. | 2.36×1010 | D. | 2.36×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数(人) | 1 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
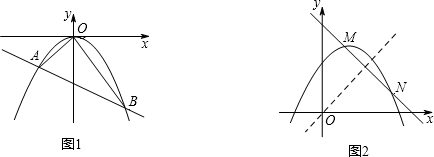
 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com