
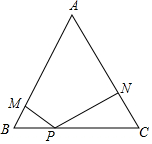
 在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.
在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.分析 (1)连接AP,过C作CD⊥AB于D,根据等边三角形的性质得到AB=AC,根据三角形的面积公式列方程即可得到结论;
(2)设BP=x,则CP=2-x,由△ABC是等边三角形,得到∠B=∠C=60°,解直角三角形得到BM=$\frac{1}{2}$x,PM=$\frac{\sqrt{3}}{2}$x,CN=$\frac{1}{2}$(2-x),PN=$\frac{\sqrt{3}}{2}$(2-x),根据二次函数的性质即可得到结论.
解答 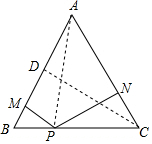 解:(1)连接AP,过C作CD⊥AB于D,
解:(1)连接AP,过C作CD⊥AB于D,
∵△ABC是等边三角形,
∴AB=AC,
∵S△ABC=S△ABP+S△ACP,
∴$\frac{1}{2}$AB•CD=$\frac{1}{2}$AB•PM+$\frac{1}{2}$AC•PN,
∴PM+PN=CD,
即不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;
(2)设BP=x,则CP=2-x,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵PM⊥AB,PN⊥AC,
∴BM=$\frac{1}{2}$x,PM=$\frac{\sqrt{3}}{2}$x,CN=$\frac{1}{2}$(2-x),PN=$\frac{\sqrt{3}}{2}$(2-x),
∴四边形AMPN的面积=$\frac{1}{2}$×(2-$\frac{1}{2}$x)•$\frac{\sqrt{3}}{2}$x+$\frac{1}{2}×$[2-$\frac{1}{2}$(2-x)]•$\frac{\sqrt{3}}{2}$(2-x)=-$\frac{\sqrt{3}}{4}$x2+$\frac{\sqrt{3}}{2}$x+$\frac{\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{4}$(x-1)2+$\frac{3\sqrt{3}}{4}$,
∴当BP=1时,四边形AMPN的面积最大,最大值是$\frac{3\sqrt{3}}{4}$.
点评 本题考查了等边三角形的性质,三角形面积的计算,二次函数的性质,正确的作出辅助线是解题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 三角形的一个外角大于任何一个内角 | |
| B. | 任意多边形的外角和都是360° | |
| C. | 三角形任一边上的中线把原三角形分成两个面积相等的三角形 | |
| D. | 三角形的中线、角平分线、高线都是线段 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
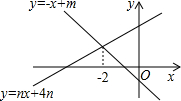 如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )
如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )| A. | -5 | B. | -4 | C. | -3 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
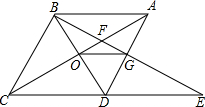 如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是①④.(把所有正确结论的序号都填在横线上)
如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是①④.(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.
学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com