
分析 (1)根据有理数的除法可以解答本题;
(2)根据有理数的除法可以解答本题;
(3)根据有理数的乘除法可以解答本题;
(4)根据有理数的乘除法可以解答本题.
解答 解:(1)(-2$\frac{1}{4}$)÷0.25
=$(-\frac{9}{4})×4$
=-9;
(2)(-24)÷(-3)÷$\frac{1}{8}$
=24÷3×8
=64;
(3)[-9]×$\frac{1}{9}$×(-1)÷(-$\frac{1}{9}$)×(-9)
=9×$\frac{1}{9}×1×9×9$
=81;
(4)(-$\frac{3}{7}$)÷$\frac{4}{7}$×(-1$\frac{1}{2}$)÷(-2$\frac{1}{4}$)
=-$\frac{3}{7}×\frac{7}{4}×\frac{3}{2}×\frac{4}{9}$
=-$\frac{1}{2}$.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
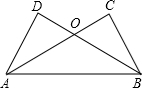 如图,AC⊥BC,BD⊥AD,要证Rt△ABC≌△BAD,需要添加一个什么条件?并在括号中说明理由
如图,AC⊥BC,BD⊥AD,要证Rt△ABC≌△BAD,需要添加一个什么条件?并在括号中说明理由查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 数量x(千克) | 1 | 2 | 3 | 4 |
| 售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com