
分析 (1)先算括号内的减法,再根据分式的乘法法则求出即可;
(2)先通分和根据多项式乘以多项式法则进行计算,再整体代入求出即可;
(3)先把除法变成乘法,合并后代入求出即可.
解答 解:(1)($\frac{x}{x-2}$-$\frac{3}{x-2}$)•$\frac{{x}^{2}-4}{x-3}$
=$\frac{x-3}{x-2}$•$\frac{(x+2)(x-2)}{x-3}$
=x+2,
当x=4时,原式=6;
(2)∵x+y=xy,
∴$\frac{1}{x}$+$\frac{1}{y}$-(1-x)(1-y)
=$\frac{1}{x}$+$\frac{1}{y}$-1+x+y-xy
=$\frac{x+y}{xy}$-1+(x+y)-xy
=1-1+xy-xy
=0;
(3)($\frac{3x}{x-2}$-$\frac{x}{x+2}$)÷$\frac{x}{{x}^{2}-4}$
=($\frac{3x}{x-2}$-$\frac{x}{x+2}$)•$\frac{(x+2)(x-2)}{x}$
=$\frac{3x}{x-2}$•$\frac{(x+2)(x-2)}{x}$-$\frac{x}{x+2}$•$\frac{(x+2)(x-2)}{x}$
=3(x+2)-(x-2)
=2x+8,
取x=1时,原式=10.
点评 本题考查了分式的混合运算和求值,能正确根据分式的运算法则进行化简是解此题的关键.


科目:初中数学 来源: 题型:解答题
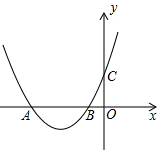 如图,抛物线y=$\frac{1}{8}$x2+3mx+18m2-m与x轴交于A(x1,0),B(x2,0)两点,且x1≠x2,与y轴交于点C.
如图,抛物线y=$\frac{1}{8}$x2+3mx+18m2-m与x轴交于A(x1,0),B(x2,0)两点,且x1≠x2,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
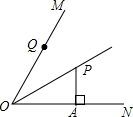 如图,OP平分∠MON,PA⊥ON,垂足为A,OA=8,PA=6,Q是射线OM上的一个动点,则线段PQ的最小值是( )
如图,OP平分∠MON,PA⊥ON,垂足为A,OA=8,PA=6,Q是射线OM上的一个动点,则线段PQ的最小值是( )| A. | 10 | B. | 8 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
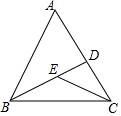 如图,已知在△ABC中,BD是角平分线,点E在BD上,连接CE,若∠BCE=25°,∠CED=55°,则∠ABC的度数为( )
如图,已知在△ABC中,BD是角平分线,点E在BD上,连接CE,若∠BCE=25°,∠CED=55°,则∠ABC的度数为( )| A. | 30° | B. | 40° | C. | 60° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
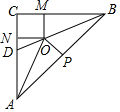 如图,已知在△ABC中,BD是角平分线,∠C=90°,∠ABC=∠BAC,O是边BD上一点,OM⊥BC于点M,ON⊥AC于点N,且OM=ON,过点O作OP⊥AB于点P.
如图,已知在△ABC中,BD是角平分线,∠C=90°,∠ABC=∠BAC,O是边BD上一点,OM⊥BC于点M,ON⊥AC于点N,且OM=ON,过点O作OP⊥AB于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com