
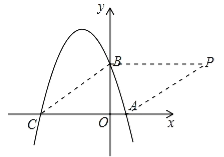
����Ŀ����֪��ͼ����ƽ��ֱ������ϵxOy�У���A��B��C�ֱ�Ϊ���������ϵ������㣬��OA=1��OB=3��OC=4��
��1����A��B��C����������ߵĽ���ʽ��
��2����ƽ��ֱ������ϵxOy���Ƿ����һ��P��ʹ�����Ե�A��B��C��PΪ������ı���Ϊ���Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3������MΪ����������һ���㣬�ڣ�2���������£��������|PM��AM|�����ֵʱ��M�����꣬��ֱ��д��|PM��AM|�����ֵ��

���𰸡���1��![]() ����2�����ڣ�P��5��3������3��M��1��0����5��
����2�����ڣ�P��5��3������3��M��1��0����5��![]() ��ʱ��|PM��AM|��ֵ���Ϊ5��
��ʱ��|PM��AM|��ֵ���Ϊ5��
����������1���������ߵĽ���ʽΪ![]() ����A��1��0����B��0��3����C����4��0������
����A��1��0����B��0��3����C����4��0������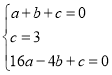 ����ã�a=
����ã�a=![]() ��b=
��b=![]() ��c=3���ྭ��A��B��C����������ߵĽ���ʽΪ
��c=3���ྭ��A��B��C����������ߵĽ���ʽΪ![]() ��
��
��2����ƽ��ֱ������ϵxOy�д���һ��P��ʹ���Ե�A��B��C��PΪ������ı���Ϊ���Σ�����Ϊ��
��OB=3��OC=4��OA=1����BC=AC=5����BPƽ���ҵ���ACʱ���ı���ACBPΪ���Σ���BP=AC=5���ҵ�P��x��ľ������OB�����P������Ϊ��5��3��������P�ڵڶ���������ʱ���Ե�A��B��C��PΪ������ı���ֻ����ƽ���ı��Σ��������Σ���P������Ϊ��5��3��ʱ���Ե�A��B��C��PΪ������ı���Ϊ���Σ�
��3����ֱ��PA�Ľ���ʽΪy=kx+b��k��0������A��1��0����P��5��3������![]() ����ã�k=
����ã�k=![]() ��b=
��b=![]() ����ֱ��PA�Ľ���ʽΪ
����ֱ��PA�Ľ���ʽΪ![]() ������M���P��A����ͬһֱ����ʱ�����������ε����߹�ϵ|PM��AM|��PA������M���P��A��ͬһֱ����ʱ��|PM��AM|=PA���൱��M���P��A��ͬһֱ����ʱ��|PM��AM|��ֵ�����MΪֱ��PA�������ߵĽ��㣬�ⷽ������
������M���P��A����ͬһֱ����ʱ�����������ε����߹�ϵ|PM��AM|��PA������M���P��A��ͬһֱ����ʱ��|PM��AM|=PA���൱��M���P��A��ͬһֱ����ʱ��|PM��AM|��ֵ�����MΪֱ��PA�������ߵĽ��㣬�ⷽ������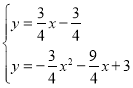 ����
����![]() ��
��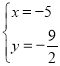 �����M��������1��0����5��
�����M������Ϊ��1��0����5��![]() ��ʱ��|PM��AM|��ֵ���ʱ|PM��AM|�����ֵΪ5��
��ʱ��|PM��AM|��ֵ���ʱ|PM��AM|�����ֵΪ5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��x2ƽ�ƣ�ʹ����λ���µ���������������һ�����������㣬д��һ�ַ��������ƽ�Ʒ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ȱߡ�ABC�Ķ���B��C������ֱ�Ϊ��2��0������6��0������N��A�������AC��C���˶�������ON��AB�ڵ�M������Mǡƽ���߶�ONʱ�����߶�CN�ij��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������-8�������ǣ� ��
A.����8��
B.������8��
C.������-8��
D.���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.�����������Ǹ���
B.��Ȳ�������Ҳ���Ǹ���
C.���������Ҳ�Ǹ���
D.������������һ���Ǹ��������Ǹ�������һ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOB�� OEƽ�֡�AOC�� OFƽ�֡�BOC.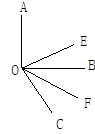
��1������AOB��ֱ�ǣ���BOC��60�㣬���EOF�Ķ�����
��2�������EOF���AOB��������ϵ��
��3������AOB����EOF��156�㣬���EOF�Ƕ��ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��1�Ƿ���x2+bx��0��һ����������������֮���ǣ�������
A.1B.��1C.0D.��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ᡢy���ཻ��B��C���㣬����D���߶�OB�ϣ����߶�DC���ŵ�D˳ʱ����ת90��õ�DE������E��ֱ��l��x����H������C��CF��y�ᣬ��ֱ��l��F�����D�ĺ�����Ϊm��
��x�ᡢy���ཻ��B��C���㣬����D���߶�OB�ϣ����߶�DC���ŵ�D˳ʱ����ת90��õ�DE������E��ֱ��l��x����H������C��CF��y�ᣬ��ֱ��l��F�����D�ĺ�����Ϊm��
��1����ֱ��д����B��C�����ꣻ
��2������E����ֱ��BC��ʱ����tan��FDE��ֵ��
��3�����ڳ���m��̽������ֱ��l���Ƿ���ڵ�G��ʹ����CDO=��DFE+��DGH�������ڣ��������G�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�У�AB=AC��D��E����BC�ϣ�Ҫʹ��ABD�ա�ACE����Ҫ����һ��������ijѧϰС���������������ʱ���������¼��ַ����� ��AD=AE����BD=CE����BE=CD���ܡ�BAD=��CAE�����п��е��У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com