
分析 (1)利用完全平方公式与单项式乘以多项式的运算法则计算,然后再合并同类项即可.
(2)先通分计算分式减法,然后将x=$\sqrt{3}$-1代入即可求得分式的值.
解答 解:(1)(a-b)2-a(a-2b)
=a2-2ab+b2-a2+2ab
=b2.
(2)原式=$\frac{2x}{(x+1)(x-1)}$-$\frac{1}{x-1}$,
=$\frac{2x}{(x+1)(x-1)}$-$\frac{x+1}{(x+1)(x-1)}$,
=$\frac{2x-x-1}{(x+1)(x-1)}$,
=$\frac{1}{x+1}$,
把x=$\sqrt{3}$-1代入,原式=$\frac{1}{\sqrt{3}-1+1}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了整式的混合运算,主要利用完全平方公式与单项式乘多项式的运算法则,熟记公式结构与运算法则是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
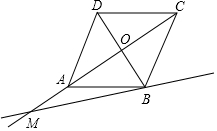 如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C,O,A都不重合),过点A,C分别向直线BM作垂线段,垂足分别为E,F,连接OE,OF.
如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C,O,A都不重合),过点A,C分别向直线BM作垂线段,垂足分别为E,F,连接OE,OF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
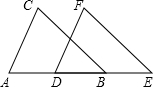 把下面的推理过程补充完整,并在括号内注明理由
把下面的推理过程补充完整,并在括号内注明理由查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com