
 如图,在一次高尔夫球比赛中,小明从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度10m时,球移动的水平距离为8m.已知山坡OA与水平方向OC的夹角为30°,OC=12m.
如图,在一次高尔夫球比赛中,小明从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度10m时,球移动的水平距离为8m.已知山坡OA与水平方向OC的夹角为30°,OC=12m.分析 (1)在Rt△ACO中,根据特殊角的三角函数值求出AC的长度,由此即可得出点A的坐标;
(2)由顶点B的坐标设球的飞行路线所在抛物线的解析式为y=a(x-8)2+10,根据点O的坐标利用待定系数法即可求出该抛物线的解析式;
(3)代入x=12,求出当x=12时,抛物线上点的纵坐标,将其与点A的纵坐标进行比较,即可得出结论.
解答 解:(1)在Rt△ACO中,∠ACO=90°,∠AOC=30°,OC=12,
∴AC=OC•tan∠AOC=12×$\frac{\sqrt{3}}{3}$=4$\sqrt{3}$,
∴点A的坐标为(12,4$\sqrt{3}$).
(2)∵顶点B的坐标为(8,10),
∴设球的飞行路线所在抛物线的解析式为y=a(x-8)2+10,
∵点O(0,0)在抛物线上,
∴0=a×(0-8)2+10,解得:a=-$\frac{5}{32}$,
∴球的飞行路线所在抛物线的解析式为y=-$\frac{5}{32}$(x-8)2+10=-$\frac{5}{32}$x2+$\frac{5}{2}$x.
(3)令y=-$\frac{5}{32}$x2+$\frac{5}{2}$x中x=12,则y=-$\frac{5}{32}$×122+$\frac{5}{2}$×12=$\frac{15}{2}$,
∵$\frac{15}{2}$≠4$\sqrt{3}$,
∴点A不在球的飞行路线所在抛物线上.
故小明这一杆不能把高尔夫球从O点直接打入球洞A点.
点评 本题考查了二次函数的应用以及待定系数法求函数解析式,解题的关键是:(1)求出AC的长;(2)利用待定系数法求出函数解析式;(3)判定点A是否在该抛物线上.本题属于中档题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出抛物线关系式是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S2012=2012$\frac{1}{2}$.Sn=$\frac{2n+1}{2}$.
如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S2012=2012$\frac{1}{2}$.Sn=$\frac{2n+1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 票 价 | 15元/人 | 13元/人 | 10元/人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
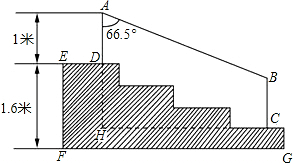 某商场门前的台阶截面如图中阴影部分所示,已知台阶有四级小台阶且每一级小台阶高度相等,台阶高度EF为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为1米的不锈钢架杆AD和BC(杆子的低端分别为D,C),且∠DAB=66.5°(cos66.5°≈0.4).
某商场门前的台阶截面如图中阴影部分所示,已知台阶有四级小台阶且每一级小台阶高度相等,台阶高度EF为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为1米的不锈钢架杆AD和BC(杆子的低端分别为D,C),且∠DAB=66.5°(cos66.5°≈0.4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com