
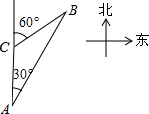
 如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( )
如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( )| A. | 40海里 | B. | 80海里 | C. | 60海里 | D. | 20海里 |
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$
如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
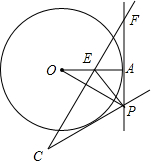 如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP
如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com