
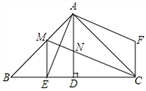
【题目】如图,![]() 中,
中,![]() 垂足是D,AE平分
垂足是D,AE平分![]() ,交BC于点E,在
,交BC于点E,在![]() 外有一点F,使
外有一点F,使![]() .
.
(1)求∠ACF的度数;
(2)求证:![]() ;
;
(3)在AB上取一点M,使![]() ,连接MC,交AD于点N,连接ME.求证:
,连接MC,交AD于点N,连接ME.求证:![]() .
.
【答案】(1)45°;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)根据等腰直角三角形的性质求出∠B=∠ACB=45°,再求出∠ACF=45°;
(2)由∠B =45°,∠ACF=45°,得到∠B=∠ACF,根据同角的余角相等求出∠BAE=∠CAF,然后利用“角边角”证明△ABE和△ACF全等,根据全等三角形对应边相等证明即可;
(3)过点E作EH⊥AB于H,求出△BEH是等腰直角三角形,然后求出HE=BH,再根据角平分线上的点到角的两边距离相等可得DE=HE,然后求出HE=HM,从而得到△HEM是等腰直角三角形,再根据等腰直角三角形的性质求解即可.
试题解析:(1)∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,∵FC⊥BC,∴∠BCF=90°,∴∠ACF=90°﹣45°=45°;
(2)∵∠B =45°,∠ACF=45°,∴∠B=∠ACF.
∵∠BAC=90°,FA⊥AE,∴∠BAE+∠CAE=90°,∠CAF+∠CAE=90°,∴∠BAE=∠CAF.
在△ABE和△ACF中,∵∠BAE=∠CAF,AB=AC,∠B=∠ACF
∴△ABE≌△ACF(ASA),∴BE=CF;
(3)如图,过点E作EH⊥AB于H,则△BEH是等腰直角三角形,∴HE=BH,∠BEH=45°.
∵AE平分∠BAD,AD⊥BC,∴DE=HE,∴DE=BH=HE.
∵BM=2DE,∴HE=HM,∴△HEM是等腰直角三角形,∴∠MEH=45°,∴∠BEM=45°+45°=90°,∴ME⊥BC.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图是某汽车维修公司的维修点在环形公路上的分布图.公司在年初分配给A,B,C,D四个维修点某种配件各50件.在使用前发现需将A,B,C,D四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次为多少?说明理由.(注:n件配件从一个维修点调整到相邻维修点的调动件次为n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,9,7,26,17,9.这组数据的众数是( )
A.17B.7C.16D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏参加了某次演讲比赛,根据比赛时七位评委所给的分数制作了如下表格:
平均数/分 | 中位数/分 | 众数/分 | 方差/分2 |
8.8 | 8.9 | 8.5 | 0.14 |
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数B.中位数C.众数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
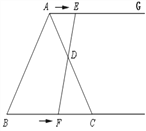
【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s) ;
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)求当t为何值时,四边形ACFE是菱形;
(3)是否存在某一时刻t,使以A、F、C、E为顶点的四边形内角出现直角?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com