
【题目】2019年12月以来,湖北省武汉市发现一种新型冠状病毒感染引起的急性呼吸道传染病.感染者的临床表现为:以发热、乏力、干咳为主要表现.约半数患者多在一周后出现呼吸困难,严重者快速进展为急性呼吸窘迫综合征、脓毒症休克、难以纠正的代谢性酸中毒和出凝血功能障碍.国家卫健委已发布1号公告,将新型冠状病毒感染的肺炎纳入传染病防治法规定的乙类传染病,但采取甲类传染病的预防、控制措施,同时将其纳入检疫传染病管理.
(1)在“新冠”初期,有2人感染了“新冠”,经过两轮传染后共有288人感染了“新冠”(这两轮感染均未被发现未被隔离),则每轮传染中平均一个人传染了几个人?
(2)某小区物管为预防业主感染传播购买![]() 型和
型和![]() 型两种
型两种![]() 口罩,购买
口罩,购买![]() 型
型![]() 口罩花费了2500元,购买
口罩花费了2500元,购买![]() 型
型![]() 口罩花费了2000元,且购买
口罩花费了2000元,且购买![]() 型
型![]() 口罩数量是购买
口罩数量是购买![]() 型
型![]() 口罩数量的2倍,已知购买一个
口罩数量的2倍,已知购买一个![]() 型
型![]() 口罩比购买一个
口罩比购买一个![]() 型
型![]() 口罩多花3元则该物业购买
口罩多花3元则该物业购买![]() 、
、![]() 两种
两种![]() 口罩的单价为多少元?
口罩的单价为多少元?
(3)由于实际需要,该物业决定再次购买这两种![]() 口罩,已知此次购进
口罩,已知此次购进![]() 型和
型和![]() 型两种
型两种![]() 口罩的数量一共为1000个,恰逢市场对这两种
口罩的数量一共为1000个,恰逢市场对这两种![]() 口罩的售价进行调整,
口罩的售价进行调整,![]() 型
型![]() 口罩售价比第一次购买时提高了
口罩售价比第一次购买时提高了![]() ,
,![]() 型
型![]() 口罩按第一次购买时售价的1.5倍出售,如果此次购买
口罩按第一次购买时售价的1.5倍出售,如果此次购买![]() 型和
型和![]() 型这两种
型这两种![]() 口罩的总费用不超过7800元,那么此次最多可购买多少个
口罩的总费用不超过7800元,那么此次最多可购买多少个![]() 型
型![]() 口罩?
口罩?
【答案】(1)每轮传染中平均一个人传染了11个人;(2)![]() 两种
两种![]() 口罩的单价分别为5、8元;(3)此次最多可购买300个
口罩的单价分别为5、8元;(3)此次最多可购买300个![]() 型
型![]() 口罩.
口罩.
【解析】
(1)设每轮传染中平均一个人传染了![]() 个人,则第一轮传染结束后,有2(1+x)人感染“新冠”,第二轮传染结束后有2(1+x)(1+x)即
个人,则第一轮传染结束后,有2(1+x)人感染“新冠”,第二轮传染结束后有2(1+x)(1+x)即![]() 人感染,可以列出方程,解方程即可;
人感染,可以列出方程,解方程即可;
(2)设该物业购买![]() 两种
两种![]() 口罩的单价分别为
口罩的单价分别为![]() ,
,![]() 元,分别表示出购买A型和B型口罩的数量,根据购买
元,分别表示出购买A型和B型口罩的数量,根据购买![]() 型
型![]() 口罩数量是购买
口罩数量是购买![]() 型
型![]() 口罩数量的2倍,列分式方程,解分式方程即可;
口罩数量的2倍,列分式方程,解分式方程即可;
(3)设该物业再次购买了![]() 个
个![]() 型,
型,![]() 个
个![]() 型
型![]() 口罩,分别表示出两种型号口罩的单价,根据总费用不超过7800元,列出不等式,解不等式求解即可.
口罩,分别表示出两种型号口罩的单价,根据总费用不超过7800元,列出不等式,解不等式求解即可.
解:(1)设每轮传染中平均一个人传染了![]() 个人,依题意得
个人,依题意得
![]()
解得![]()
因为传染的人数不能为负,
所以![]() 应舍去,
应舍去,
所以每轮传染中平均一个人传染了11个人.
(2)设该物业购买![]() 两种
两种![]() 口罩的单价分别为
口罩的单价分别为![]() ,
,![]() 元,依题意得
元,依题意得
![]()
解得![]()
经检验:![]() 是原分式方程的根,并符合题目的实际意义
是原分式方程的根,并符合题目的实际意义
![]() 种
种![]() 口罩的单价为:
口罩的单价为:![]() 元
元
所以![]() 两种
两种![]() 口罩的单价分别为5元、8元
口罩的单价分别为5元、8元
(3)设该物业再次购买了![]() 个
个![]() 型,
型,![]() 个
个![]() 型
型![]() 口罩,依题意得
口罩,依题意得
![]()
解得![]()
所以此次最多可购买300个![]() 型
型![]() 口罩.
口罩.


科目:初中数学 来源: 题型:
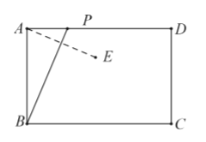
【题目】如图1和图2,矩形ABCD中,E是AD的中点,P是BC上一点,AF∥PD,∠FPE=∠DPE.
(1)作射线PE交直线AF于点G,如图1.
①求证:AG=DP;
②若点F在AD下方,AF=2,PF=7,求DP的长.
(2)若点F在AD上方,如图2,直接写出PD,AF,PF的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展征文活动,征文主题只能从“爱国”、“敬业”、“诚信”、“友善”四个主题中选择一个,每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是_____度;
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有______名;
(4)学生会宣传部有七年级的2名男生和2名女生,现从中随机挑选2名同学参加“主题征文”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一动点,点
上一动点,点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,在点
的对称点,在点![]() 的运动过程中有且只有一个点
的运动过程中有且只有一个点![]() 到线段
到线段![]() 的距离为4,则
的距离为4,则![]() 的取值范围是____________.
的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
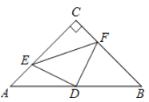
【题目】如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E,F分别在AC,BC上运动,(点E不与点A,C重合),且保持AE=CF,连接DE,EF,再次运动变化过程中,有下列结论:①四边形CEDF有可能成为正方形;②△DFE是等腰直角三角形;③四边形CEDF的面积是定值.其中正确的结论是:______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
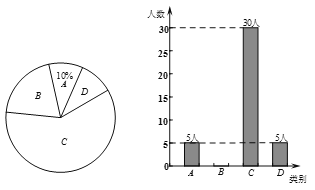
【题目】为了解阳光社区年龄20~60岁居民对垃圾分类的认识,学校课外实践小组随机抽取了该社区、该年龄段的部分居民进行了问卷调查,并将调查数据整理后绘成如下两幅不完整的统计图.图中A表示“全部能分类”,B表示“基本能分类”,C表示“略知一二”,D表示“完全不会”.请根据图中信息解答下列问题:
(1)补全条形统计图并填空:被调查的总人数是 人,扇形图中D部分所对应的圆心角的度数为 ;
(2)若该社区中年龄20~60岁的居民约3000人,请根据上述调查结果,估计该社区中C类有多少人?
(3)根据统计数据,结合生活实际,请你对社区垃圾分类工作提一条合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点的直线与反比例函数![]() (k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.
(k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com