
 轴上,腰OA=4.
轴上,腰OA=4.
 轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;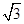 ,2),(-4,0)(3)
,2),(-4,0)(3) =-
=-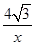
 轴于C点.………………………………2分
轴于C点.………………………………2分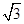 ,……………………………4分
,……………………………4分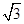 ,2).………………………………………………5分
,2).………………………………………………5分 轴的对称点
轴的对称点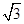 ,2),………………………………………………6分
,2),………………………………………………6分 轴的对称点B1的坐标为(-4,0);…………………………7分
轴的对称点B1的坐标为(-4,0);…………………………7分 =
= ,……………………………8分
,……………………………8分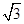 ,2)代入解析式,
,2)代入解析式,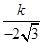 ,∴
,∴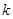 =-4
=-4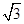 ,………………………………………………9分
,………………………………………………9分 =-
=-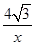 .…………………………………10分
.…………………………………10分 轴于C点,根据解直角三角形求出OC的长,从而求出A、B两点坐标,再根据对称性求出A1与B1的坐标
轴于C点,根据解直角三角形求出OC的长,从而求出A、B两点坐标,再根据对称性求出A1与B1的坐标

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:不详 题型:解答题
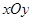 中,直线AB与反比例函数
中,直线AB与反比例函数 的图像交于点A(-3,4),AC⊥
的图像交于点A(-3,4),AC⊥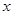 轴于点C.
轴于点C.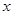 轴的交点为B(a,0),并与反比例函数
轴的交点为B(a,0),并与反比例函数 图象的另一支还有一个交点的情形下,求△ABC的面积S与
图象的另一支还有一个交点的情形下,求△ABC的面积S与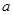 之间的函数关系式.并写出自变量
之间的函数关系式.并写出自变量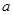 的取值范围.
的取值范围.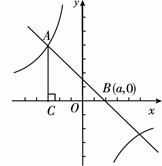
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
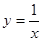 ,下列结论中不正确的是( )
,下列结论中不正确的是( )| A.图象经过点(-1,-1) |
| B.图象在第一、三象限 |
| C.两个分支关于原点成中心对称 |
D.当x<0时,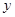 随着 随着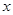 的增大而增大 的增大而增大 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
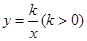 的图象经过点A(3,m),过点A作
的图象经过点A(3,m),过点A作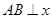 轴于点B,
轴于点B, 的面积为
的面积为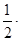
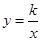 的图象上,求当
的图象上,求当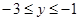 时,对应的x的取值范围;
时,对应的x的取值范围;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图像相交于点M(2,m),N(一l,n),若y1>y2,则x的取值范围是( )
的图像相交于点M(2,m),N(一l,n),若y1>y2,则x的取值范围是( )
| A.x< -1或O<x<2 | B.x<-1或x>2 |
| C. -l<x<0或O<x<2 | D.-l<x<0或x>2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 交于A、B两点,P、Q分别是
交于A、B两点,P、Q分别是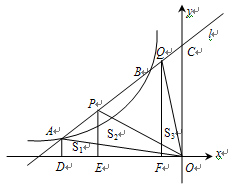
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com