
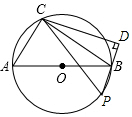
 如图,已知⊙O的直径AB=4,点C在⊙O上,AC=2,动点P在半圆弧$\widehat{AB}$上运动(不与A、B两点重合),点P、C在直径AB的异侧,连接PB、PC,过点C作直线PB的垂线段CD,垂足为点D.
如图,已知⊙O的直径AB=4,点C在⊙O上,AC=2,动点P在半圆弧$\widehat{AB}$上运动(不与A、B两点重合),点P、C在直径AB的异侧,连接PB、PC,过点C作直线PB的垂线段CD,垂足为点D.分析 (1)由AC=$\frac{1}{2}$AB,求得∠ABC=30°,继而可得∠CPD=∠A=60°,求出∠PCD的度数;
(2)根据当CP是直径时,△PCD与△ABC全等作图;
(3)由(1)易求得∠PCD的度数,又由垂径定理,可求得∠ACP的度数,求出∠BCD的度数,根据垂径定理和勾股定理求出线段CD的长.
解答 解:(1)∠PCD的度数不变.
∵AB是直径,
∴∠ACB=90°,又AC=$\frac{1}{2}$AB,
∴∠ABC=30°,
∴∠A=90°-∠ABC=60°,
∴∠CPD=∠A=60°,又CD⊥PB,
∴∠PCD=30°;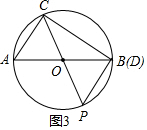
(2)如图3:当CP=AB,即CP为⊙O的直径时,△PCD与△ABC全等;
(3)如图2,∵∠A=60°,
∴∠BPC=∠A=60°,
∵CD⊥PB,
∴∠PCD=90°-∠BPC=30°,
∵CP⊥AB,AB是⊙O的直径,
∴$\widehat{AC}$=$\widehat{AP}$,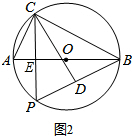
∴∠ACP=∠ABC=30°,
∴∠BCD=∠ACB-∠ACP-∠PCD═90°-30°-30°=30°,
∵∠ACB=90°,AB=4,AC=2,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
∵∠ACB=90°,CP⊥AB,
∴$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AB×CE,
解得,CE=$\sqrt{3}$,
∵CP⊥AB,
∴CP=2CE=2$\sqrt{3}$,又∠P=60°,
∴CD=CP×$\frac{\sqrt{3}}{2}$=3.
点评 此题考查了圆周角定理、垂径定理以及含30°角的直角三角形的性质,掌握同弧所对的圆周角相等、30°所对的直角边是斜边的一半是解题的关键,解答时注意数形结合思想的应用.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
| 1⊙3=1×4+3=7 | 3⊙(-1)=3×4-1=11 |
| 5⊙4=5×4+4=24 | 4⊙(-3)=4×4-3=13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小王骑自行车锻炼,以每小时10公里的速度,从A地前往30公里远的B地,到达B地后即以每小时15公里的速度返回A地.设自行车与A地相距y(公里),所花时间为x(小时).
小王骑自行车锻炼,以每小时10公里的速度,从A地前往30公里远的B地,到达B地后即以每小时15公里的速度返回A地.设自行车与A地相距y(公里),所花时间为x(小时).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com