
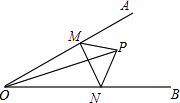
 如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,求MN的长.
如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,求MN的长. 分析 设点P关于OA的对称点为C,关于OB的对称点为D,当点M、N在CD上时,△PMN的周长最小,此时△COD是等边三角形,设MQ=x,则PM=CM=3-x,根据勾股定理得到x,进一步求得MN的长.
解答 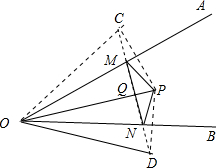 解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PC、PD.
解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PC、PD.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=6,
∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=6.
∵∠POC=∠POD,
∴OP⊥CD,
∴OQ=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴PQ=6-3$\sqrt{3}$,
设MQ=x,则PM=CM=3-x,
∴(3-x)2-x2=(6-3$\sqrt{3}$)2,解得x=6$\sqrt{3}$-9.
则MN=2x=18$\sqrt{3}$-18.
点评 本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质;熟练掌握轴对称的性质,证明三角形是等边三角形是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
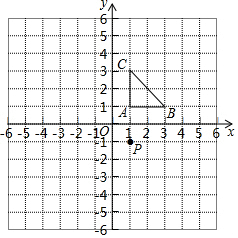 在平面直角坐标系中,小方格都是边长为1的正方形,△ABC≌△DEF,其中点A、B、C都在格点上,请你解答下列问题:
在平面直角坐标系中,小方格都是边长为1的正方形,△ABC≌△DEF,其中点A、B、C都在格点上,请你解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠β和线段a,c.
如图,已知∠β和线段a,c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com