
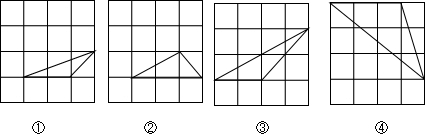
| A、①③ | B、①② | C、②③ | D、②④ |
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
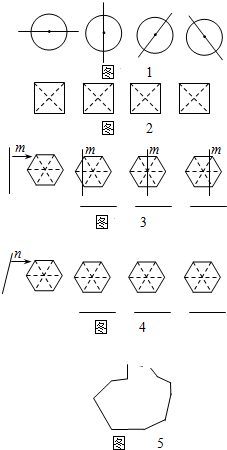 (2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).
(2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).查看答案和解析>>
科目:初中数学 来源:课堂三级讲练数学九年级(上) 题型:013
如图,5个全等的正六边形A、B、C、D、E,请仔细观察A、B、C、D四个图案,其中与E图案也完全相同的是
[ ]
|
A. |
B. |
|
C. |
D. |
|
E. |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江乐清育英寄宿学校九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,四个正六边形的面积都是6,则图中△ABC的面积等于(??? ).
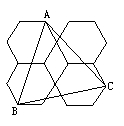
A.12????????? B. 13??????? C.14?????????? D.15
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:解答题
如图,抛物线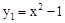 交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
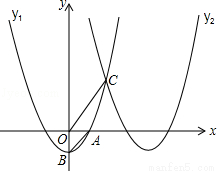
(1)请直接写出抛物线y2的解析式;
(2)若点P是x轴上一动点,且满足∠CPA=∠OBA,求出所有满足条件的P点坐标;
(3)在第四象限内抛物线y2上,是否存在点Q,使得△QOC中OC边上的高h有最大值?若存在,请求出点Q的坐标及h的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com