
【题目】如图1,平移三角形ABD,使点D沿BD的延长线平移至点C,得到三角形△A'B'D',A'B'交AC于点E,AD平分∠BAC.
(1)猜想∠B'EC与∠A'之间的关系,并写出理由;
(2)如果将三角形ABD平移至如图2所示位置,得到△A'B'D',请问:A'D'平分∠B'A'C吗?为什么?
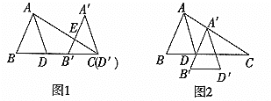
【答案】(1)∠B'EC=2∠A';理由见解析;(2)A'D'平分∠B'A'C,理由见解析.
【解析】
(1)根据角平分线的性质得出∠BAD=∠DAC,根据平移的性质得出∠BAD=∠A',AB∥A'B',进而得出∠BAC=∠B'EC,即可得出答案;
(2)利用平移的性质得出∠B'A'D'=∠BAD,AB∥A'B',进而得出∠BAD![]() ∠BAC,即可得出∠B'A'D'
∠BAC,即可得出∠B'A'D'![]() ∠B'A'C.
∠B'A'C.
(1)∠B'EC=2∠A'.理由如下:
∵AD平分∠BAC,∴∠BAD=∠DAC.
∵将△ABD平移,使D沿BD延长线移至C得到△A'B'D',A'B'交AC于E,∴∠BAD=∠A',AB∥A'B',∴∠BAC=∠B'EC,∴∠BAD=∠A'![]() ∠BAC
∠BAC![]() ∠B'EC,即∠B'EC=2∠A';
∠B'EC,即∠B'EC=2∠A';
(2)A'D'平分∠B'A'C.理由如下:
∵将△ABD平移至如图(2)所示,得到△A'B'D',∴∠B'A'D'=∠BAD,AB∥A'B',∴∠BAC=∠B'A'C.
∵∠BAD![]() ∠BAC,∴∠B'A'D'
∠BAC,∴∠B'A'D'![]() ∠B'A'C,∴A'D'平分∠B'A'C.
∠B'A'C,∴A'D'平分∠B'A'C.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点 A1、A2、A3、…在射线 ON 上,点 B1、B2、B3、…在射线 OM 上;△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形.若 OA1=1,则△A2015B2015A2016 的边长为 ( )
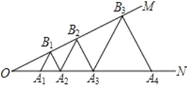
A. 4028 B. 4030 C. 22014 D. 22015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
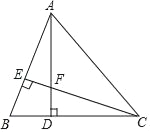
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,寻找对顶角(不含平角).
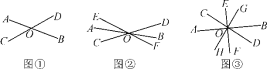
(1)如图①,图中共有______对对顶角;
(2)如图②,图中共有______对对顶角;
(3)如图③,图中共有______对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成__________对对顶角;
(5)若20条直线相交于一点,则可形成对顶角多少对?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,PC切⊙O于C,AE⊥PC交PC的延长线于E,AE交⊙O于D,PC与AB的延长线相交于点P,连接AC、BC.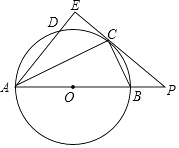
(1)求证:AC平分∠BAD;
(2)若PB:PC=1:2,PB=4,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点.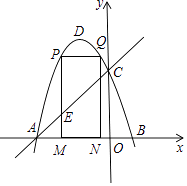
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=2 ![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com