
| A. | -1 | B. | $\sqrt{11}$ | C. | $\frac{3}{7}$ | D. | $\root{3}{8}$ |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
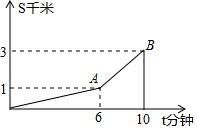 小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:
小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
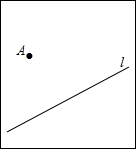 点A表示某村的一个蓄水池,l表示一条小河,为了将河水引入蓄水池,现在决定修建一条引水管道,请你在图中画出修建的这条管道的最短路线.并说明理由:
点A表示某村的一个蓄水池,l表示一条小河,为了将河水引入蓄水池,现在决定修建一条引水管道,请你在图中画出修建的这条管道的最短路线.并说明理由:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-a>1-b | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | $\frac{a}{b}<1$ | D. | $-\frac{1}{3}a>-\frac{1}{3}b$. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com