
 如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )
如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )| A. | BC=$\sqrt{3}$CD | B. | ∠A=90° | C. | AD=BC | D. | AB∥CD |
分析 A、根据条件不能确定∠BAD的度数,所以添加此条件,不能推出四边形ABCD是矩形;
B、先根据两组对边分别平行证明其是平行四边形,再由有一个角是直角的平行四边形,可得矩形;
C、先根据一组对边平行且相等可得其是平行四边形,同理可得矩形;
D、直接根据两组对边分别平行证明其是平行四边形,再由有一个角是直角的平行四边形,可得矩形.
解答 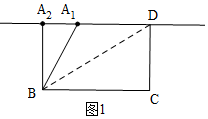 解:A、如图1,∵AD∥BC,∠D=90°,
解:A、如图1,∵AD∥BC,∠D=90°,
∴∠C=90°,
连接BD,
tan∠DBC=$\frac{DC}{BC}$,
∵BC=$\sqrt{3}$CD,
∴tan∠DBC=$\frac{CD}{\sqrt{3}CD}$=$\frac{\sqrt{3}}{3}$,
∴∠DBC=30°,
如图1所示,点A不确定,∠BAD不一定等于90°,可以组成矩形,也可以组成其他四边形,
所以添加选项A不能推出四边形ABCD是矩形;
B、如图2,∵∠D=90°,∠A=90°,
∴∠A+∠D=180°,
∴AB∥DC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵∠D=90°,
∴?ABCD是矩形,
所以添加选项B可以推出四边形ABCD是矩形;
C、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵∠D=90°,
∴?ABCD是矩形,
所以添加选项C可以推出四边形ABCD是矩形;
D、∵AD∥BC,AB∥CD,
∴∴四边形ABCD是平行四边形,
∵∠D=90°,
∴?ABCD是矩形,
所以添加选项D可以推出四边形ABCD是矩形;
故选A.
点评 本题考查了矩形的判定、平行四边形的判定,熟练掌握矩形的判定是关键,常运用“有一个角是直角的平行四边形是矩形”这一方法来判定.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
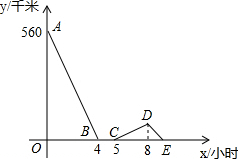 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
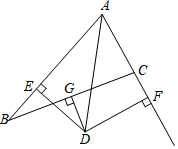 如图,在△ABC中,AB=7,AC=3,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F,下列说法正确的是( )
如图,在△ABC中,AB=7,AC=3,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F,下列说法正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | $\sqrt{4}$ | C. | $\sqrt{2}$ | D. | 3.14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com