
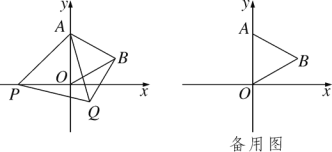
【题目】如图,在平面直角坐标系中,已知点A(0,4),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由;
(3)连接OQ,当OQ∥AB时,求点P的坐标.
【答案】(1)B(![]() );(2)∠ABQ=90°,始终不变,理由详见解析;(3)P(
);(2)∠ABQ=90°,始终不变,理由详见解析;(3)P(![]() )
)
【解析】
(1)过点B作BC⊥x轴于点C,证明∠BOC=30°,OB=4,借助含30°的直角三角形的性质以及勾股定理可求出BC,OC的长,从而可解决问题;
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题;
(3)根据AB∥OQ,得出∠BQO=90°,∠BOQ=∠ABO=60°,从而可求出BQ的长,再根据(2)中△APO≌△AQB得出PO=BQ,即可得出结果.
解:(1)如图1,过点B作BC⊥x轴于点C,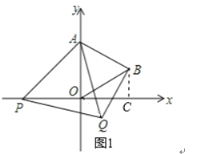
∵△AOB为等边三角形,且OA=4,
∴∠AOB=60°,OB=OA=4,
∴∠BOC=30°,而∠OCB=90°,
∴BC=![]() OB=2,∴OC=
OB=2,∴OC=![]() ,
,
∴点B的坐标为B(2![]() ,2);
,2);
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ,AO=AB,∠PAQ=∠OAB,
∴∠PAO=∠QAB,
在△APO与△AQB中,
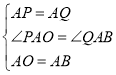 ,
,
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)如图2,∵点P在x轴负半轴上,点Q在点B的下方,AB∥OQ,∠ABQ=90°,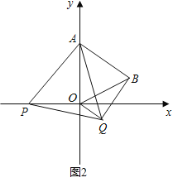
∴∠BQO=90°,∠BOQ=∠ABO=60°,
∴∠OBQ=30°,
又∵OB=4,
∴OQ=2,
∴BQ=![]() ,
,
由(2)可知,△APO≌△AQB,
∴OP=BQ=2![]() ,
,
∴此时点P的坐标为(-2![]() ,0).
,0).


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
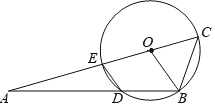
【题目】如图,以△AOB 的顶点 O 为圆心,OB 为半径作⊙O,交 OA 于点 E,交 AB 于点 D,连接 DE,DE∥OB,延长 AO 交⊙O 于点 C,连接 CB.
(1)求证:![]() ;
;
(2)若 AD=4![]() ,AE=CE,求 OC 的长.
,AE=CE,求 OC 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
数据段 | 频数 | 频率 |
30~40 | 10 | 0.05 |
40~50 | 36 | |
50~60 | 0.39 | |
60~70 | ||
70~80 | 20 | 0.10 |
总计 | 200 | 1 |
注:30~40为时速大于等于30千米而小于40千米,其他类同
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
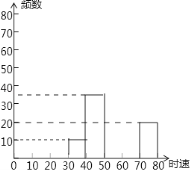
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
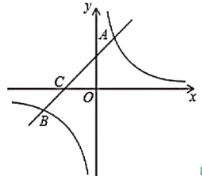
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、象限内的
的图象相交于第一、象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)长为2的线段![]() 在射线
在射线![]() 上左右移动,若射线
上左右移动,若射线![]() 上存在三个点
上存在三个点![]() 使得
使得![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
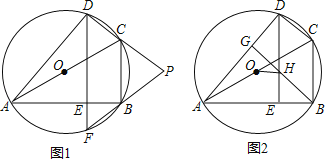
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 分别在菱形
分别在菱形![]() 的边
的边![]() 上滑动(点
上滑动(点![]() 不与
不与![]() 重合),且
重合),且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 与
与![]() 不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
(3)如图3,若![]() ,请直接写出四边形
,请直接写出四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
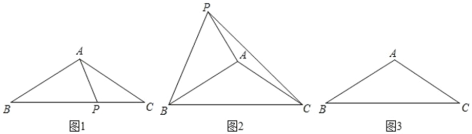
【题目】等腰△ABC 中,AB=AC,∠BAC=120°,点 P 为平面内一点.
(1)如图 1,当点 P 在边 BC 上时,且满足∠APC=120°,求![]() 的值;
的值;
(2)如图 2,当点 P 在△ABC 的外部,且满足∠APC+∠BPC=90°,求证:BP=![]() AP;
AP;
(3)如图 3,点 P 满足∠APC=60°,连接 BP,若 AP=1,PC=3,直接写出BP 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy 中,直线![]() 与x轴交于点A,与过点B(0,2)且平行于x轴的直线l交于点C,点A关于直线l的对称点为点D.
与x轴交于点A,与过点B(0,2)且平行于x轴的直线l交于点C,点A关于直线l的对称点为点D.
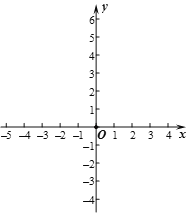
(1)求点C、D的坐标;
(2)将直线![]() 在直线l上方的部分和线段CD记为一个新的图象G.若直线
在直线l上方的部分和线段CD记为一个新的图象G.若直线![]() 与图象G有两个公共点,结合函数图象,求b的取值范围.
与图象G有两个公共点,结合函数图象,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com