
【题目】如图,在平面直角坐标系中,已知A、B分别是x轴上位于原点左右两侧的点,点P在第一象限,且它的纵坐标为3,直线AP交y轴于点C(0,2),直线PB交y轴于点D,且ΔAOP的面积为6.

(1)求直线AP的关系式;
(2)若ΔBOP与ΔAOP的面积相等,求ΔBOD的面积.
【答案】(1)直线AP的关系式为y=![]() (2)12
(2)12
【解析】
(1)先根据ΔAOP的面积为6, 点P的纵坐标为3求出A点的坐标,再用待定系数法求出直线AP的关系式即可.
(2)ΔBOP与ΔAOP的面积相等,则OA=OB,可求出B点坐标,根据直线AP的关系式和P点的纵坐标可确定P点的坐标,用待定系数法求出直线BD的解析式,进而确定D点坐标,最后求ΔBOD的面积.
(1)根据题意得:
![]()
∴OA=4
故A点坐标为(-4,0)
设直线AP的关系式为y=kx+b,代入A(-4,0)C(0,2)得:
![]() 解得
解得![]()
∴直线AP的关系式为y=![]()
(2)若ΔBOP与ΔAOP的面积相等,
则OA=OB,故B的坐标为(4,0)
把y=3代入y=![]() 得:x=2
得:x=2
∴P点的坐标为(2,3)
设直线BD的解析式为y=mx+n,把B(4,0),P(2,3)代入得:
![]() 解得
解得
故直线BD的解析式为y=![]()
∴D点的坐标为(0,6)
∴ΔBOD的面积=![]()


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
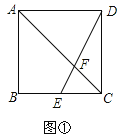
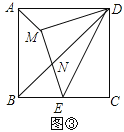
【题目】如图,点E是矩形ABCD的边BC的中点,连接DE交AC于点F.
![]() 如图
如图![]() ,求证:
,求证:![]() ;
;
![]() 如图
如图![]() ,作
,作![]() 于G,试探究:当AB与AD满足什么关系时,使得
于G,试探究:当AB与AD满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
![]() 如图
如图![]() ,以DE为斜边在矩形ABCD内部作等腰
,以DE为斜边在矩形ABCD内部作等腰![]() ,交对角线BD于N,连接AM,若
,交对角线BD于N,连接AM,若![]() ,请直接写出
,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图,回答下列问题(1)机动车行驶________小时后加油,中途加油_______升;(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并直接写出自变量t的取值范围;(3)如果加油站距目的地还有230千米,车速为40千米/时,要到达目的地,油箱中的油是否够用?请说明理由。
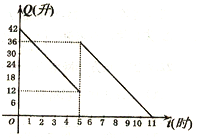
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)直接写出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x (h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车出发多长时间后,两车恰好相距40km?
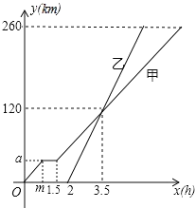
查看答案和解析>>
科目:初中数学 来源: 题型:
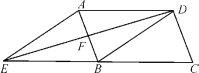
【题目】如图,在平行四边形ABCD中,DB=DA,∠ADB的平分线交AB于点F,交CB的延长线于点E,连接AE.
(1)求证:四边形AEBD是菱形;
(2)若DC=![]() ,EF:BF=3,求菱形AEBD的面积.
,EF:BF=3,求菱形AEBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
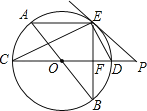
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c所表示的数在数轴上的位置如图所示:
![]()
(1)化简:│a-1│-│c+b│+│b-1│;
(2)若a+b+c=0,且b与-1的距离和c与-1的距离相等,求:-a2+2b-c-(a-4c-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
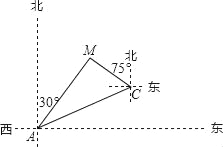
【题目】如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达C处,测得小区M位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,并求AN的长.(精确到1米,![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com