
【题目】如图:AB=AC,AD=AE,AB⊥AC,AD⊥AE。
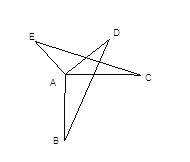
(1)求证:△EAC≌△DAB
(2)判断线段EC与线段BD的关系,并说明理由
【答案】(1)证明见详解;(2)BD⊥CE,理由见详解.
【解析】
(1)根据垂直的定义可得∠BAC=∠DAE=90°,然后求出∠BAD=∠CAE,再利用“边角边”证明△ABD和△ACE全等;
(2)根据全等三角形对应角相等可得∠B=∠C,然后利用三角形的内角和定理求出∠BFC=∠BAC=90°,再根据垂直的定义证明即可.
证明:如图,
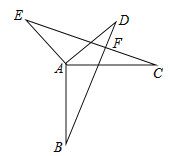
(1)∵AB⊥AC,AD⊥AE,
∴∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△ABD和△ACE中,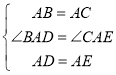 ,
,
∴△ABD≌△ACE(SAS);
(2)BD⊥CE
理由:∵△ABD≌△ACE,
∴∠B=∠C,
又∵∠B+∠BAC=∠C+∠BFC,
∴∠BFC=∠BAC=90°,
∴BD⊥CE.


科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.

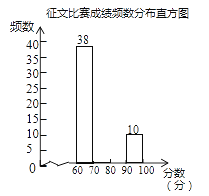
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE⊥AB,BD⊥AC,垂足分别为E、D,BD、CE交于点O,AB=AC,∠B=20°,则∠AOD=( )

A. 20°B. 40°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2)
﹣2)
请解答:
(1)![]() 整数部分是 ,小数部分是 .
整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求|a﹣b|+
的整数部分为b,求|a﹣b|+![]() 的值.
的值.
(3)已知:9+![]() =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列三个结论: ①∠AOB=90°+![]() ;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab,其中正确的是( )
;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab,其中正确的是( )
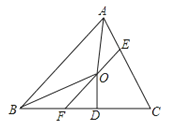
A. ①②③B. ①③C. ①②D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月第18号台风“泰利”给某地造成严重影响.草根救援队驾若冲锋舟沿一条东西方向的河流营救灾民,早晨从![]() 地出发,晚上最后到达
地出发,晚上最后到达![]() 地,约定向东为正方向,当天航行依次记录如下(单位:千米)
地,约定向东为正方向,当天航行依次记录如下(单位:千米) ![]() 问:
问:
(1)![]() 地在
地在![]() 地的东面,还是西面?与
地的东面,还是西面?与![]() 地相距多少千米?
地相距多少千米?
(2)若冲锋舟每千米耗油0.5升,每升汽油需6.8元,问冲锋舟工作一天需汽油费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查适合做抽样调查的是![]()
![]()
A. 检查一枚用于发射卫星的运载火箭的各零部件
B. 对某社区的卫生死角进行调查
C. 对某班学生进行6月5日式“世界环境日”知晓情况的调查
D. 对中学生目前的睡眠情况进行调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,网格线是由边长为1的小正方形格子组成的,小正方形的顶点叫做格点,以格点为顶点的多边形叫做格点多边形.小明与数学小组的同学研究发现,内部含有3个格点的四边形的面积与该四边形边上的格点数有某种关系,请你观察图中的4个格点四边形.设内部含有3个格点的四边形的面积为![]() ,其各边上格点的个数之和为
,其各边上格点的个数之和为![]() ,则
,则![]() 与
与![]() 之间的关系式为__________.
之间的关系式为__________.
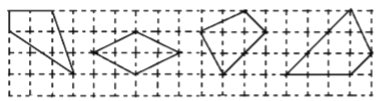
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com