
【题目】我们规定,若关于 x 的一元一次方程 ax=b 的解为 x=ba,则称该方程的为差解方程,例如:3x=![]() 的解为x=
的解为x=![]() 且
且![]() =
=![]() -3,则该方程3x=
-3,则该方程3x=![]() 就是差解方程.
就是差解方程.
请根据以上规定解答下列问题
(1)若关于 x 的一元一次方程-5x=m+1 是差解方程,则 m=_____.
(2)若关于 x 的一元一次方程 2x=ab+3a+1 是差解方程,且它的解为 x=a,求代数式(ab+2)2019的值.
科目:初中数学 来源: 题型:
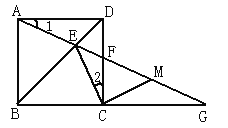
【题目】如图,正方形ABCD中,E是BD上一点,AE的延长线交CD于F,交BC的延长线于G,M是FG的中点.
(1)求证:① ∠1=∠2;② EC⊥MC.
(2)试问当∠1等于多少度时,△ECG为等腰三角形?请说明理由.
【答案】(1)①证明见解析;②证明见解析;(2)当∠1=30°时,△ECG为等腰三角形. 理由见解析.
【解析】试题分析:(1)①根据正方形的对角线平分一组对角可得![]() 然后利用边角边定理证明
然后利用边角边定理证明![]() ≌
≌![]() 再根据全等三角形对应角相等即可证明;
再根据全等三角形对应角相等即可证明;
②根据两直线平行,内错角相等可得![]() 再根据直角三角形斜边上的中线等于斜边的一半可得
再根据直角三角形斜边上的中线等于斜边的一半可得![]() 然后据等边对等角的性质得到
然后据等边对等角的性质得到![]() ,所以
,所以![]() 然后根据
然后根据![]() 即可证明
即可证明![]() 从而得证;
从而得证;
(2)根据(1)的结论,结合等腰三角形两底角相等![]() 然后利用三角形的内角和定理列式进行计算即可求解.
然后利用三角形的内角和定理列式进行计算即可求解.
试题解析:(1)证明:①∵四边形ABCD是正方形,
∴∠ADE=∠CDE,AD=CD,
在△ADE与△CDE,
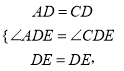
∴△ADE≌△CDE(SAS),
∴∠1=∠2,
②∵AD∥BG(正方形的对边平行),
∴∠1=∠G,
∵M是FG的中点,
∴MC=MG=MF,
∴∠G=∠MCG,
又∵∠1=∠2,
∴∠2=∠MCG,
∵![]()
∴![]()
∴EC⊥MC;
(2)当∠1=30°时, ![]() 为等腰三角形. 理由如下:
为等腰三角形. 理由如下:
∵![]() 要使
要使![]() 为等腰三角形,必有
为等腰三角形,必有![]()
∴![]() span>
span>
∵![]()
∴![]()
∴![]()
∴∠1=30°.
【题型】解答题
【结束】
24
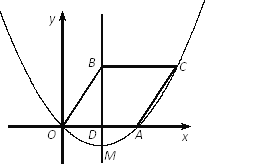
【题目】如图,已知抛物线经过原点O和点A,点B(2,3)是该抛物线对称轴上一点,过点B作BC∥x轴交抛物线于点C,连结BO、CA,若四边形OACB是平行四边形.
(1)① 直接写出A、C两点的坐标;② 求这条抛物线的函数关系式;
(2)设该抛物线的顶点为M,试在线段AC上找出这样的点P,使得△PBM是以BM为底边的等腰三角形并求出此时点P的坐标;
(3)经过点M的直线把□ OACB的面积分为1:3两部分,求这条直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
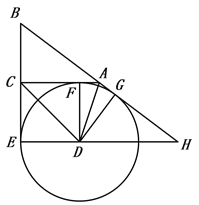
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,⊙
,⊙![]() 与
与![]() 、
、![]() 、
、![]() 都相切,切点分别是
都相切,切点分别是![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两个根.
的两个根.
(1)求证:![]() 是直角三角形;
是直角三角形;
(2)若![]() ,求四边形CEDF的面积.
,求四边形CEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
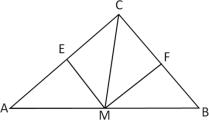
【题目】如图,在![]() 中,
中,![]() ,M是AB中点,
,M是AB中点,![]() ,
,
(1)在AE、EF、FB中是否总有最大的线段?若有,是哪一条?
(2)AE、EF、FB能否构成直角三角形?若能,请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:课本上有这样一道例题:“解方程:![]()
解:去分母得:
6(x+15)=15-10(x-7)①
6x+90=15-10x+70②
16x=-5③
x=-![]() ④
④
请回答下列问题:
(1)得到①式的依据是________;
(2)得到②式的依据是________;
(3)得到③式的依据是________;
(4)得到④式的依据是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,节约资源,从今年6月1日起国家禁止超市、商场、药店为顾客提供免费塑料袋,为解决顾客购物包装问题,心连心超市提供了A自带购物袋;B租借购物篮;C购买环保袋;D徒手携带,四种方式供顾客选择.该超市把6月1日、2日两天的统计结果绘成如图的条形统计图和6月1日的扇形统计图,请你根据图形解答下列问题:
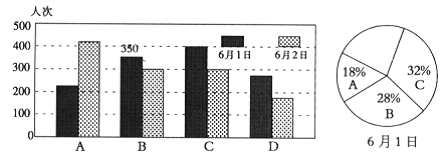
(1)请将6月1日的扇形统计图补充完整.
(2)根据统计图求6月1日在该超市购物总人次和6月1日自带购物袋的人次.
(3)比较两日的条形图,你有什么发现?请用一句话表述你的发现.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所研制了一种抗生素新药,据临床观察:如果成人按规定的剂量注射这种抗生素,那么注射药液后每毫升血液中的含药量![]() 与时间
与时间![]() 之间的关系近似地满足如图所示的折线.
之间的关系近似地满足如图所示的折线.
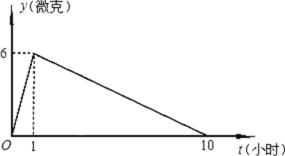
(1)写出注射药液后,每毫升血液中含药量![]() 与时间
与时间![]() 之间的函数解析式及自变量的取值范围;
之间的函数解析式及自变量的取值范围;
(2)据临床观察:每毫升血液中含药量不少于![]() 时,对控制病情是有效的,如果病人按规定的剂量注射该药液后,那么这一次注射的药液经过多长时间后控制病情开始有效?这个有效时间是多长?
时,对控制病情是有效的,如果病人按规定的剂量注射该药液后,那么这一次注射的药液经过多长时间后控制病情开始有效?这个有效时间是多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com