
 在△ABC中,∠C=90°,CD⊥AB于D,AC=15,DB=16,求AD和BC的长.
在△ABC中,∠C=90°,CD⊥AB于D,AC=15,DB=16,求AD和BC的长. 分析 根据射影定理得AC2=AD•AB,即152=AD(AD+16),解得AD=9或AD=-25(舍去),然后再利用射影定理得到BC2=BD•BA,再利用算术平方根求BC.
解答 解:∵∠C=90°,CD⊥AB于D,
∴AC2=AD•AB,
即152=AD(AD+16),
整理得AD2+16AD-225=0,解得AD=9或AD=-25(舍去),
∵BC2=BD•BA,
∴BC=$\sqrt{16×(9+16)}$=20,
∴AD和BC的长分别为9,20.
点评 本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:选择题
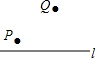 如图,直线1表示石家庄的太平河,点P表示朱河村,点Q表示黄庄村,欲在太平河1上修建一个水泵站(记为点M),分别向两村供水,现有如下四种修建水泵站供水管道的方案,图中实线表示修建的管道,则修建的管道最短的方案是( )
如图,直线1表示石家庄的太平河,点P表示朱河村,点Q表示黄庄村,欲在太平河1上修建一个水泵站(记为点M),分别向两村供水,现有如下四种修建水泵站供水管道的方案,图中实线表示修建的管道,则修建的管道最短的方案是( )| A. | 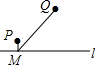 | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
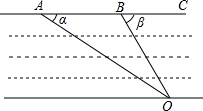 如图,要测量一段两岸平行的河的宽度,在A点测得∠α=30°,在B点测得∠β=60°,且AB=50米,则这段河岸的宽度为25$\sqrt{3}$米.
如图,要测量一段两岸平行的河的宽度,在A点测得∠α=30°,在B点测得∠β=60°,且AB=50米,则这段河岸的宽度为25$\sqrt{3}$米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com