
分析 (1)根据平方差中的第一个奇数表示为2n+1,则第二个奇数表示为2n-1,可以表示出规律的一般形式;
(2)根据平方差公式:(a-b)(a+b)=a2-b2证明即可得到答案.
解答 解:①72-52=8×3;②92-72=8×4;
③112-92=8×5;④132-112=8×6;
(1)解:根据各个算式的规律可以得到,
(2n+1)2-(2n-1)2=8n,
(2)证明:(2n+1)2-(2n-1)2
=(2n+1+2n-1)(2n+1-2n+1)
=8n.
故答案为:3,7,11,11.
点评 本题考查的是根据算式总结规律和运用平方差公式进行证明的问题,正确表示相应的奇数、熟练运用平方差公式:(a-b)(a+b)=a2-b2是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
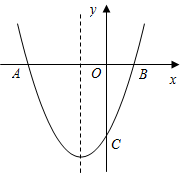 已知:抛物线的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0)、C(0,-2).
已知:抛物线的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0)、C(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
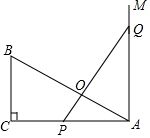 如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.
如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E,则下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E,则下列结论错误的是( )| A. | BD+ED=BC | B. | ED+AC>AD | C. | DA平分∠EDC | D. | DE平分∠ADB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com