
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��0��a����B��b��a������a��b���㣨a��3��2+|b��6|��0����ͬʱ����A��B�ֱ�����ƽ��3����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��AB��

��1�����C��D�����꼰�ı���ABDC�����S�ı���ABCD��
��2����y�����Ƿ����һ��M������MC��MD��ʹS��MCD��![]() S�ı���ABCD������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
S�ı���ABCD������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
��3����P��ֱ��BD�ϵ�һ�����㣬����PA��PO������P��BD���ƶ�ʱ������B��D�غϣ���ֱ��д����BAP����DOP����APO֮�������������ϵ��
���𰸡���1��18����2��M��0��2����0����2������3���ٵ���P���߶�BD���ƶ�ʱ����APO����DOP+��BAP���ڵ���P��DB���ӳ�����ʱ����DOP����BAP+��APO���۵���P��BD���ӳ�����ʱ����BAP����DOP+��APO��
��������
��1�����ݷǸ��������ʷֱ����a��b������ƽ�ƹ��ɵõ���C��D�����꣬����������ͼ�ε��������S�ı���ABCD��
��2����M����Ϊ��0��m�������������ε������ʽ�г����̣��ⷽ�����m���õ���M�����ꣻ
��3���ֵ�P���߶�BD�ϡ���P��DB���ӳ����ϡ���P��BD���ӳ������������������ƽ���ߵ����ʽ��
�⣺��1���ߣ�a��3��2+|b��6|��0��
��a��3��0��b��6��0��
����ã�a��3��b��6��
��A��0��3����B��6��3����
�߽���A��B�ֱ�����ƽ��3����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D��
��C����2��0����D��4��0����
��S�ı���ABDC��AB��OA��6��3��18��
��2����y���ϴ���һ��M��ʹS��MCD��S�ı���ABCD��
��M������0��m����
��S��MCD��![]() S�ı���ABDC��
S�ı���ABDC��
��![]() ��6|m|��
��6|m|��![]() ��18��
��18��
���m����2��
��M��0��2����0����2����
��3���ٵ���P���߶�BD���ƶ�ʱ����APO����DOP+��BAP��
�������£���ͼ1������P��PE��AB��
��CD��ABƽ�Ƶõ�����CD��AB��
��PE��CD��
���BAP����APE����DOP����OPE��
���BAP+��DOP����APE+��OPE����APO��
�ڵ���P��DB���ӳ�����ʱ��ͬ�ٵķ����ã�
��DOP����BAP+��APO��
�۵���P��BD���ӳ�����ʱ��ͬ�ٵķ����ã�
��BAP����DOP+��APO��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ҰѶԽ����ഹֱ���ı��ν����������ı��Ρ���
��1������̽������ͼ1����֪�ı���ABCD�У�AC��BD������ΪO����֤��AB2+CD2��AD2+BC2��
��2��������⣺��֪AB��5��BC��4���ֱ��ԡ�ABC�ı�BC��AB����������Rt��BCQ�͵���Rt��ABP��
����ͼ2������ACB��90�㣬����PQ����PQ��
����ͼ3������ACB��90�㣬��M��N�ֱ���AC��AP�е�����MN����MN��![]() ����S��ABC���� ����
����S��ABC���� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ͽ����ݼܵ�ʾ��ͼ�����ݼ���BC��AC��BA��AD�Ķν������Ϻ��Ӷ��ɣ�����A��B��C��D�ĵ��Ϊ���ӵ㣬��AB=AC��DΪBC���е㣬���躸��������Ķν��������ѽغã����ѱ��BC�ε��е�D����ô��������ӹ�����ֻ�пɼ���ֱ�ǵĽdzߣ�����Ϊ��ȷ���ٵغ��ӣ���Ӧ������ѡȡ�����ν������ϼ����ӵ��ǣ�������
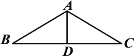
A.AB��AD����AB.AB��AC����B
C.AC��BC, ��CD.AD��BC����D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y = x2 - 4x + 3��
��1�����䷽����y = x2 - 4x + 3����y = a(x - h)2 + k����ʽ��
��2����ƽ��ֱ������ϵ![]() �л����ú�����ͼ��
�л����ú�����ͼ��
��3����0��x��3ʱ��y��ȡֵ��Χ�� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���BAD=80����AB�Ĵ�ֱƽ���߽��Խ���AC�ڵ�F������ΪE������DF������CDF���ڣ���
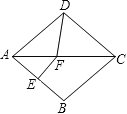
A.50��B.60��C.70��D.80��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�Ҵ��㹺������װ��ѧУ����ҵ����᳡�������������Ц���Ͱ������֣���������ļ۸�ͬ����ͬһ������ļ۸���ͬ.���ڻ᳡������Ҫ������ʱ��һ����4������Ϊ��λ����֪��һ����������ļ۸���ͼ��ʾ�������������ļ۸�Ϊ______Ԫ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ��ֱ������ϵ����һ��![]() .
.
��1������![]() ��
��![]() ��ľ���Ϊ2ʱ�����
��ľ���Ϊ2ʱ�����![]() �����ꣻ
�����ꣻ
��2������![]() ��������
��������![]() ����
����![]() ��ʱ�����
��ʱ�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���![]() �У���
�У���![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ���е㣻��
���е㣻��![]() ��
�� ![]() Ϊ
Ϊ![]() �����ȷֵ㣬
�����ȷֵ㣬 ![]() ��
�� ![]() Ϊ
Ϊ![]() �����ȷֵ�.С��ֱ��ò�ͬ�ķ�ʽ���Ӿ��ζԱ��ϵĵ㣬��ͼ2��ͼ3��ʾ.��ô��ͼ2���ı���
�����ȷֵ�.С��ֱ��ò�ͬ�ķ�ʽ���Ӿ��ζԱ��ϵĵ㣬��ͼ2��ͼ3��ʾ.��ô��ͼ2���ı���![]() �������ͼ3���ı���
�������ͼ3���ı���![]() ����������
����������
��1��С���̽����������
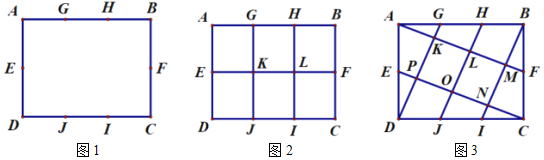
��ͼ2�У�С���֣� ![]() ��
��
��ͼ3�У�С����ı���![]() �����̽������. ���㽫С���˼·��д������
�����̽������. ���㽫С���˼·��д������
��![]() ��
�� ![]()
��![]()
��![]() �������Ʊ�Ϊ
�������Ʊ�Ϊ![]() ���õ�
���õ�![]()
��![]()
��![]() �������Ʊ�Ϊ
�������Ʊ�Ϊ![]() ���õ�
���õ�![]()
�֡�![]() ��
�� ![]()
��![]()
��![]() ��
�� ![]() ��
�� ![]()
��![]() ����
����![]() �����
�����![]() ������
������![]() ����
����![]() ����
����
��2��С���ְ���ͼ4�ķ�ʽ���Ӿ���![]() �Ա��ϵĵ�.��
�Ա��ϵĵ�.��![]() .
.
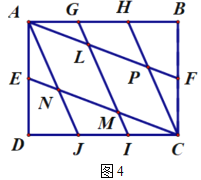
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A���ʾ��a��B���ʾ��b��AB��ʾA���B��֮��ľ��룬C��AB���е㣬��a��b����|a+3|+��b+3a��2=0��
��1�����C��ʾ������
��2����P��A����3����λÿ�������˶�����Qͬʱ��B����2����λÿ�������˶�����AP+BQ=2PQ����ʱ��t��
��3������P��A�����˶�����MΪAP�е㣬��P�㵽���B֮ǰ����![]() ��ֵ���䣻��2BM��BP��ֵ���䣬����ֻ��һ����ȷ�������ҳ���ȷ�Ľ��۲������ֵ��
��ֵ���䣻��2BM��BP��ֵ���䣬����ֻ��һ����ȷ�������ҳ���ȷ�Ľ��۲������ֵ��
![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com