练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．计算：$\frac{3}{2}\sqrt{6}×（-\sqrt{\frac{1}{2}}÷\sqrt{2\frac{1}{4}}）$．

    分析 直接利用二次根式乘除运算法则化简求出答案．

    解答 解：原式=$\frac{3}{2}$$\sqrt{6}$×（-$\sqrt{\frac{1}{2}×\frac{4}{9}}$）
    =-$\frac{3}{2}$$\sqrt{6}$×$\frac{\sqrt{2}}{3}$
    =-$\sqrt{3}$．

    点评 此题主要考查了二次根式的乘除运算，正确化简二次根式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．下列说法正确的是（　　）
    A．事件“任意一个x（x为实数）值，x2是不确定事件”
    B．已知某篮球运动员投篮投中的概率为0.6，则他投十次一定投中6次
    C．为了了解我市各超市销售的速冻食品质量情况，适合采取普查的方式调查
    D．投掷一枚质地均匀的硬币10次，可能有5次正面向上

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知关于x的一元二次方程x2-6x+2m+1=0有实数根．
    （1）求实数m的取值范围；
    （2）若方程的两个实数根为x1，x2，且x1x2+x1+x2=15，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知如图1菱形ABCD，∠ABC=60°，边长为 3，在菱形内作等边三角形△AEF，边长为2$\sqrt{2}$，点E，点F，分别在AB，AC上，以A为旋转中心将△AEF顺时针转动，旋转角为α，如图2

    （1）在图2中证明BE=CF；
    （2）若∠BAE=45°，求CF的长度；
    （3）当CF=$\sqrt{17}$时，直接写出旋转角α的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

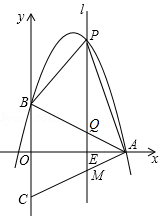    11．如图，在等腰△ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=ax2+$\frac{7}{2}$x+c经过A（8，0）、B（0，4）两点．
    （1）求抛物线的解析式；
    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段CA、OA、AB和抛物线于点M、E、Q和点P，连接PA、PB，设直线l移动的时间为t（0＜t＜4）秒，当t为何值时，线段PQ最长？
    （3）在（2）的条件下，抛物线上是否存在一点P，使△PAM的内角为直角？若存在，请直接写出点P的坐标；若不存在，请说明理由．（温馨提示：若直线y=k1x+b1与直线y=k2x+b2垂直，则k1•k2=-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知a=2$\sqrt{3}$，b=3$\sqrt{2}$，则a与b的大小关系为a＜b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．某水果公司购进10 000kg苹果，公司想知道苹果的损坏率，从所有苹果中随机抽取若干进行统计，部分结果如下表：
    苹果总质量n（kg）1002003004005001000
    损坏苹果质量m（kg）10.5019.4230.6339.2449.54101.10
    苹果损坏的频率$\frac{m}{n}$（结果保留小数点后三位）0.1050.0970.1020.0980.0990.101
    估计这批苹果损坏的概率为0.1（结果保留小数点后一位），损坏的苹果约有1000kg．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．（1）问题背景
    如图①，BC是⊙O的直径，点A在⊙O上，AB=AC，P为BmC上一动点（不与B，C重合），求证：$\sqrt{2}$PA=PB+PC．
    小明同学观察到图中自点A出发有三条线段AB，AP，AC，且AB=AC，这就为旋转作了铺垫．于是，小明同学有如下思考过程：
    第一步：将△PAC绕着点A顺时针旋转90°至△QAB（如图①）；
    第二步：证明Q，B，P三点共线，进而原题得证．
    请你根据小明同学的思考过程完成证明过程．
    （2）类比迁移
    如图②，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=AC，AB⊥AC，垂足为A，求OC的最小值．
    （3）拓展延伸
    如图③，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=$\frac{4}{3}$AC，AB⊥AC，垂足为A，则OC的最小值为$\frac{3}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

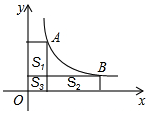    6．如图，A、B是双曲线y=$\frac{k}{x}$上的点，分别过A、B两点作x轴、y轴的垂线段．S1，S2，S3分别表示图中三个矩形的面积，若S3=1，且S1+S2=4，则k=3．

    查看答案和解析>>

    同步练习册答案