
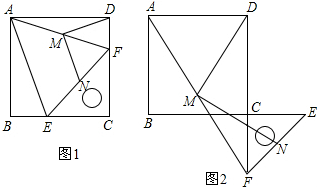
���� ��1�����������ε������Լ�����ֱ�������ε�֪ʶ֤����CE=CF���̶�֤������ABE�ա�ADF���õ�AE=AF��֤������AEF�ǵ��������Σ�
��2������ֱ��������б�������ߵ������Լ������ε���λ�ߵ����ʿɵõ�MN��MD��������ϵ��Ȼ�������ε���ǵ����ʺ�ȫ�������ε�����֤����DMF=��BAE+��DAF���Ӷ���֤����DMN=��DAB=90�㣻
��3������AE����MD�ڵ�G����dz������ǣ�����֤����MN��AE��MN=${\frac{1}{2}}_{\;}$AE�����ɣ�1���Ľ����Լ��ǽ�֮���������ϵ�õ���DMN=��DGE=90�㣮
��� ��1��֤�������ı���ABCD�������Σ�
��AB=AD=BC=CD����B=��ADF=90�㣮
�ߡ�CEF�ǵ���ֱ�������Σ���C=90�㣬
��CE=CF��
��BC-CE=CD-CF����BE=DF��
���ڡ�ABE�͡�ADF��$\left\{\begin{array}{l}{AB=AD}\\{��B=��D}\\{BE=DF}\end{array}\right.$��
���ABE�ա�ADF��
��AE=AF��
���AEF�ǵ��������Σ�
��2��DM=MN��DM��MN��
���ɣ�����Rt��ADF��DM��б��AF�����ߣ�
��AF=2DM��
��MN�ǡ�AEF����λ�ߣ�
��AE=2MN��
��AE=AF��
��DM=MN��
�ߡ�DMF=��DAF+��ADM��AM=MD��
�ߡ�FMN=��FAE����DAF=��BAE��
���ADM=��DAF=��BAE��
���DMN=��BAD=90�㣬
��DM��MN��
��3��������
���ɣ�����AE����MD�ڵ�G��
�ߵ�MΪAF���е㣬��NΪEF���е㣬
��MN��AE��MN=$\frac{1}{2}$AE��
���ı���ABCD�������Σ�
��AB=AD=BC=CD����B=��ADF=90�㣮
�ߡ�CEF�ǵ���ֱ�������Σ���C=90�㣬
��CE=CF��
��BC+CE=CD+CF����BE=DF��
���ڡ�ABE�͡�ADF��$\left\{\begin{array}{l}{AB=AD}\\{��B=��D}\\{BE=DF}\end{array}\right.$��
���ABE�ա�ADF��
��AE=AF����1=��2��
����Rt��ADF�У���MΪAF���е㣬
��DM=$\frac{1}{2}$AF��
��DM=MN��
��AB��DF��AD��BE��
���1=��3����2=��4��
���3=��4��
��DM=AM��
���MAD=��5��
���DGE=��5+��4=��MAD+��3=90�㣮
��MN��AE��
���DMN=��DGE=90�㣮
��DM��MN��
���� ������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ���������ε����ʡ�����ֱ�������ε����ʡ�ֱ��������б���ϵ����ߵ����ʡ������ε���λ�ߵ������Լ�ȫ�������ε����ʺ��ж���֤�á�DMN=90���ǽ���Ĺؼ���


 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 90�� | B�� | 100�� | C�� | 110�� | D�� | 105�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -22=2-2 | B�� | -22=��$\frac{1}{2}$��-2 | C�� | ��-2��-2=22 | D�� | ��-2��-2=��$\frac{1}{2}$��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
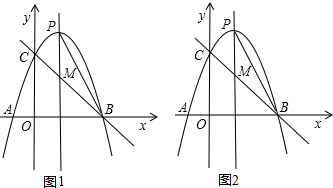
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���� | 4��1�� | 4��2�� | 4��3�� | 4��4�� | 4��5�� | 4��6�� | 4��7�� |
| ���� | 27�� | 30�� | 29�� | 28�� | 17�� | 16�� | 17�� |
| A�� | 10��28 | B�� | 14��17 | C�� | 14��27 | D�� | 14��28 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com