
分析 (1)按照规律写出x14即可.
(2)当x=-3时,|x+x1+x2+x3+…+x20|的值最小,由此可以解决问题.
解答 解:①由题意:x1=2,x2=3,x3=4,x4=5,x5=6,x6=7,x7=4,x8=5,x9=6,x10=7,x11=4,x12=5,x13=6,x14=7.
故答案为x14=7.
②特殊值法:
当x=-6时,可得|x+x1+x2+x3+…+x20|=44,
当x=-5时,可得|x+x1+x2+x3+…+x20|=39,
当x=-4时,可得|x+x1+x2+x3+…+x20|=34,
当x=-3时,可得|x+x1+x2+x3+…+x20|=33,
当x=-2时,可得|x+x1+x2+x3+…+x20|=32,
当x=-1时,可得|x+x1+x2+x3+…+x20|=31,
当x=0时,可得|x+x1+x2+x3+…+x20|=30,
综上所述,x=0时,|x+x1+x2+x3+…+x20|的值最小,此时x3=-1
故答案为-1.
点评 本题考查规律型:图形的变化,解题的关键是连接题意,利用规律解决问题,可以取特殊值尝试一下,找到x为何值时|x+x1+x2+x3+…+x20|的值最小,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 如图,在同一个平面直角坐标系xOy中,虚半圆O是函数y=$\sqrt{25-{x}^{2}}$(-5≤x≤5)的图象,实曲线(两支)是函数y=$\frac{k}{|x|}$(k≠0)的图象:已知方程$\sqrt{25-{x}^{2}}$=$\frac{k}{|x|}$(k≠0)有一个解为x=-3,则该方程其余的解为3、4、-4.
如图,在同一个平面直角坐标系xOy中,虚半圆O是函数y=$\sqrt{25-{x}^{2}}$(-5≤x≤5)的图象,实曲线(两支)是函数y=$\frac{k}{|x|}$(k≠0)的图象:已知方程$\sqrt{25-{x}^{2}}$=$\frac{k}{|x|}$(k≠0)有一个解为x=-3,则该方程其余的解为3、4、-4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
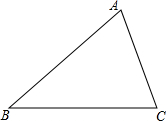 如图,锐角角形ABC中,BC>AB>AC,小骏同学按照下列步骤作图:
如图,锐角角形ABC中,BC>AB>AC,小骏同学按照下列步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
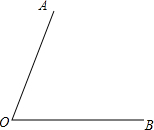 己知∠AOB=70°,根据语句画图,并填空
己知∠AOB=70°,根据语句画图,并填空查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\root{3}{(-3)^{3}}$=3 | D. | $\sqrt{(3.14-π)^{2}}$=π-3.14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com