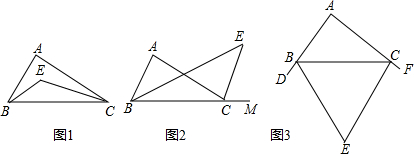
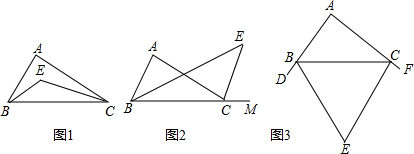
(1)证明:∵BE、CE分别平分∠ABC和∠ACB,
∴∠EBC=

∠ABC,∠ECB=

∠ACB(角平分线的定义)
∴∠BEC=180°-(∠EBC+∠ECB)( 三角形内角和定理)
=180°-(
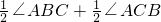
),
=180°-

(∠ABC+∠ACB),
=180°-

(180°-∠A),
=180°-90°+

∠A,
=90°+
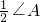
;
(2)探究2结论:∠BEC=

∠A,
理由如下:
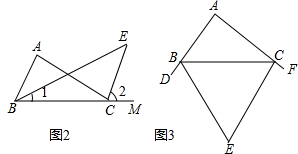
∵BE和CE分别是∠ABC和∠ACM的角平分线,
∴∠1=

∠ABC,∠2=

∠ACM,
又∵∠ACM是△ABC的一外角,
∴∠ACM=∠A+∠ABC,
∴∠2=

(∠A+∠ABC)=

∠A+∠1,
∵∠2是△BEC的一外角,
∴∠BEC=∠2-∠1=

∠A+∠1-∠1=

∠A;
(3)探究3:∠EBC=

(∠A+∠ACB),∠ECB=

(∠A+∠ABC),
∠BEC=180°-∠EBC-∠ECB,
=180°-

(∠A+∠ACB)-

(∠A+∠ABC),
=180°-

∠A-

(∠A+∠ABC+∠ACB),
结论∠BEC=90°-

∠A.
分析:(1)根据题目解答过程填写即可;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠E与∠1表示出∠2,然后整理即可得到∠BEC与∠E的关系;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠EBC与∠ECB,然后再根据三角形的内角和定理列式整理即可得解.
点评:本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.

 ∠A.
∠A. ∠ABC,∠ECB=
∠ABC,∠ECB= ∠ACB(角平分线的定义)
∠ACB(角平分线的定义)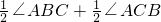 )=180°-
)=180°- (∠ABC+∠ACB)
(∠ABC+∠ACB) (180°-∠A)
(180°-∠A)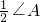
 ∠ABC,∠ECB=
∠ABC,∠ECB= ∠ACB(角平分线的定义)
∠ACB(角平分线的定义)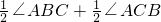 ),
), (∠ABC+∠ACB),
(∠ABC+∠ACB), (180°-∠A),
(180°-∠A), ∠A,
∠A,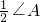 ;
; ∠A,
∠A,
 ∠ABC,∠2=
∠ABC,∠2= ∠ACM,
∠ACM, (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠1,
∠A+∠1, ∠A+∠1-∠1=
∠A+∠1-∠1= ∠A;
∠A; (∠A+∠ACB),∠ECB=
(∠A+∠ACB),∠ECB= (∠A+∠ABC),
(∠A+∠ABC), (∠A+∠ACB)-
(∠A+∠ACB)- (∠A+∠ABC),
(∠A+∠ABC), ∠A-
∠A- (∠A+∠ABC+∠ACB),
(∠A+∠ABC+∠ACB), ∠A.
∠A.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案