【题目】如图，点A是半径为3的⊙O上的点，
尺规作图：作⊙O的内接正六边形ABCDEF；
求
中弧AC的长．
【答案】（1）见解析；（2）2π
【解析】试题分析：（1）由正六边形ABCDEF的中心角为60°，可得△OAB是等边三角形，继而可得正六边形的边长等于半径，则可画出⊙O的内接正六边形ABCDEF；
（2）由（1）可求得∠AOC=120°，继而求得（1）中
的长．
试题解析：（1）首先连接OA，然后以A为圆心，OA长为半径画弧，交⊙O于B，F，再分别以B，F为圆心，OA长为半径画弧，交⊙O于点E，C，在以C为圆心，OA长为半径画弧，交⊙O于点D，则正六边形ABCDEF即为所求；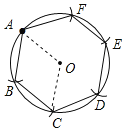
（2）∵正六边形ABCDEF是⊙O的内接正六边形
∴∠AOC=
×2=120°，
∵⊙O的半径为3，
∴
的长为： 
=2π．
科目：初中数学 来源： 题型：
【题目】进价为每件40元的某商品，售价为每件50元时，每星期可卖出500件，市场调查反映：如果每件的售价每降价1元，每星期可多卖出100件，但售价不能低于每件42元，且每星期至少要销售800件．设每件降价x元 （x为正整数），每星期的利润为y元．
（1）求y与x的函数关系式并写出自变量x的取值范围；
（2）若某星期的利润为5600元，此利润是否是该星期的最大利润？说明理由．
（3）直接写出售价为多少时，每星期的利润不低于5000元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示,在长方形ABCD中,AB=CD=8cm,AD=BC=6cm,点E是DC边上一点,且CE=1cm,动点P从A点出发,沿折线A-D-E以acm/s的速度向终点E运动,运动时间为t秒,已知a是方程
的解.
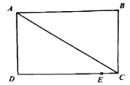
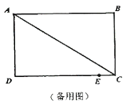
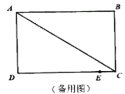
(1)求a的值；
(2)点P在运动过程中,请用t的式子表示△APC的面积；
(3)在点P运动的同时,有一动点Q从C点出发,沿折线C-D-A以1cm/s的速度向终点A运动,运动过程中,一个点停止运动时另一个点继续向终点运动,当△APC和△AQC的面积相差6平方厘米时,求t的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
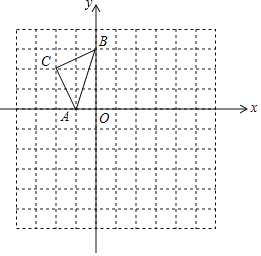
【题目】如图，在已知的平面直角坐标系中，△ABC的顶点都在正方形网格的格点上，若A，B两点的坐标分别是A（-1，0），B（0，3）．
（1）将△ABC绕原点O顺时针旋转90°得到△A1B1C1，画出△A1B1C1；
（2）以点O为位似中心，与△ABC位似的△A2B2C2满足A2B2：AB=2：1，请在网格内画出△A2B2C2，并直接填写△A2B2C2的面积为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，甲、乙、丙、丁、戊五名同学有以下说法：甲说：“直线BC不过点A”；乙说：“点A在直线CD外”； 丙说：“D在线段CB的反向延长线上；”丁说：“A，B，C，D两两连结，有5条线段” ； 戊说：“射线AD与射线CD不相交”． 其中说明正确的有（ ）．
A. 3人B. 4人C. 5人D. 2人
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（﹣1，1）、B（0，﹣2）、C（1，0），点P（0，2）绕点A旋转180°得到点
，点绕点B旋转180°得到点
，点绕点C旋转180°得到点
，点绕点A旋转180°得到点
，…，按此作法进行下去，则点
的坐标为( )
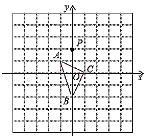
A.（0，4）B.（﹣2，0）C.（2，﹣4）D.（﹣2，﹣2）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，3），B（2，5），C（4，2）（每个方格的边长均为1个单位长度）
（1）将△ABC平移，使点A移动到点A1，请画出△A1B1C1；
（2）作出△ABC关于O点成中心对称的△A2B2C2，并直接写出A2，B2，C2的坐标；
（3）△A1B1C1与△A2B2C2是否成中心对称？若是，请写出对称中心的坐标；若不是，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
1637 年笛卡儿(R．Descartes，1596 1650)在其《几何学》中，首次应用待定系数法将 4 次方程分解为两个 2 次方程求解，并最早给出因式分解定理．
他认为，若一个高于二次的关于 x 的多项式能被 (
) 整除，则其一定可以分解为 () 与另外一个整式的乘积，而且令这个多项式的值为 0 时， x = a 是关于 x 的这个方程的一个根．
例如：多项式
可以分解为 (
) 与另外一个整式 M 的乘积，即 
令
时，可知 x =1 为该方程的一个根．
关于笛卡尔的“待定系数法”原理，举例说明如下： 分解因式：
观察知，显然 x=1 时，原式 = 0 ，因此原式可分解为 () 与另一个整式的积．
令：
，则=
，因等式两边 x 同次幂的系数相等，则有：
，得
，从而
此时，不难发现 x= 1 是方程 
的一个根．
根据以上材料，理解并运用材料提供的方法，解答以下问题：
（1）若
是多项式
的因式，求 a 的值并将多项式分解因式；
（2）若多项式
含有因式及
，求a+ b 的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．
（1）求证：BG=DE；
（2）若E为AD中点，FH=2，求菱形ABCD的周长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com