
 如图,在等边△ABC的BC边为直径画半圆,分别交AB、AC于点E、D,等边三角形的边长是8.在边AB上取一点F,使AF=2,连接FD.求证:
如图,在等边△ABC的BC边为直径画半圆,分别交AB、AC于点E、D,等边三角形的边长是8.在边AB上取一点F,使AF=2,连接FD.求证:分析 (1)连结BD,根据圆周角定理得出∠BDC=90°,再根据等边三角形的三线合一的性质得AD=DC=4,∠C=∠A=∠B=60°,进而得出$\frac{AD}{BC}$=$\frac{AF}{DC}$=$\frac{1}{2}$,证得△AFD∽△CDB,证得∠AFD=∠CDB=90°,从而证得结论;
(2)连接OD,根据三角形中位线的性质定理证得OD∥AB,即可证得OD⊥DF,从而证得DF是半圆的切线.
解答  解:(1)连接BD,
解:(1)连接BD,
∵BC是直径,
∴BD⊥AC,
∵△ABC是等边三角形,
∴AD=DC=4,∠A=∠C=60°
∵AF=2,BC=8,
∴$\frac{AD}{BC}$=$\frac{AF}{DC}$=$\frac{1}{2}$,
∴△AFD∽△CDB,
∴∠AFD=∠CDB=90°,
∴△AFD是直角三角形;
(2)连接OD,
∵AD=DC,BO=CO,
∴OD∥AB,
∴∠ODF+∠BFD=180°,
∵∠AFD=∠BFD=90°,
∴∠FDO=90°,
∴OD⊥DF,
∴DF是半圆的切线.
点评 本题考查了圆周角定理,等边三角形的性质,三角形相似的判定和性质,平行线的判定和性质,切线的判定等,熟练掌握性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:填空题
已知抛物线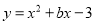 ,请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间,你确定的b的值是_______。
,请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间,你确定的b的值是_______。
查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:单选题
已知一组数据-1,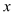 ,0,1,-2的平均数是0,那么这组数据的方差是( )
,0,1,-2的平均数是0,那么这组数据的方差是( )
A. 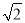 B. 2 C. 4 D. 10
B. 2 C. 4 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com