
【题目】如图所示,ABCD中,E,F分别是AB、CD上的点,AE=CF,M、N分别是DE、BF的中点.
(1)求证:四边形ENFM是平行四边形.
(2)若∠ABC=2∠A,求∠A的度数.

【答案】(1)见解析;(2)∠A=60°
【解析】
(1)先证△ADE≌△CBF(SAS),得DE=BF,∠AED=∠CFB,进而得ME=FN,∠AED=∠ABF,即ME∥FN,由此得证;
(2)由平行线的性质得∠A+∠ABC=180°,据此计算得解.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C.
又∵AE=CF,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,DE=BF,
由四边形ABCD是平行四边形,
∴DC∥AB.
∴∠CFB=∠ABF.
∴∠AED=∠ABF.
∴ME∥FN,
又∵M、N分别是DE、BF的中点,且DE=BF,
∴ME=FN.
∴四边形ENFM是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴∠A+∠ABC=180°,
又∵∠ABC=2∠A,
∴3∠A=180°,
∴∠A=60°.


科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.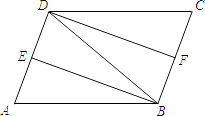
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.

小题1:如图1,可以求出阴影部分的面积是_______ (写成两数平方差的形式);
小题2:如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______,长是______,面积是_________ (写成多项式乘法的形式).
小题3:比较图 1,图2的阴影部分面积,可以得到乘法公式________ (用式子表达).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )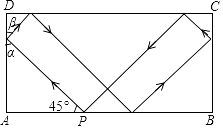
A.16
B.16 ![]()
C.20
D.20 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
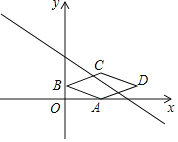
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),对角线BD与x轴平行,若直线y=kx+5+2k(k≠0)与菱形ABCD有交点,则k的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.﹣2≤k≤2且k≠0
D.﹣2≤k≤2且k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=ax2+bx+4与x轴交于A(﹣3,0),B两点,与y轴交于点C,点M(﹣ ![]() ,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com