
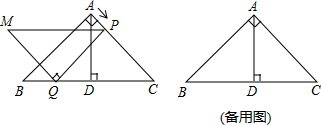
���� ��1������M����AB��ʱ���ı���AMQP�������Σ���ʱ��D���Q�غϣ��ɴ˼��ɽ�����⣮
��2����ͼ1�У�����M����AD��ʱ����PE��QC��E����֤��DQ=QE=EC����PE��AD����$\frac{PA}{AC}$=$\frac{DE}{DC}$=$\frac{2}{3}$���ɴ˼��ɽ�����⣮
��3�����������ٵ�0��x��4ʱ����ͼ2�У���PM��PQ�ֱ�AD�ڵ�E��F�����ص�����Ϊ��PEF���ڵ�4��x��$\frac{16}{3}$ʱ����ͼ3�У���PM��MQ�ֱ�AD��E��G�����ص�����Ϊ�ı���PEGQ���۵�$\frac{16}{3}$��x��8ʱ����ͼ4�У����غϲ���Ϊ��PMQ���ֱ���㼴�ɽ�����⣮
��� �⣺��1������M����AB��ʱ���ı���AMQP�������Σ���ʱ��D���Q�غϣ�AP=CP=4$\sqrt{2}$������x=$\frac{4\sqrt{2}}{\sqrt{2}}$=4��
�ʴ�Ϊ4��
��2����ͼ1�У�����M����AD��ʱ����PE��QC��E��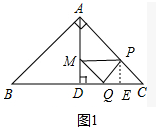
�ߡ�MQP����PQE����PEC���ǵ���ֱ�������Σ�MQ=PQ=PC
��DQ=QE=EC��
��PE��AD��
��$\frac{PA}{AC}$=$\frac{DE}{DC}$=$\frac{2}{3}$����AC=8$\sqrt{2}$��
��PA=$\frac{16\sqrt{2}}{3}$��
��x=$\frac{16\sqrt{2}}{3}$��$\sqrt{2}$=$\frac{16}{3}$��
�ʴ�Ϊ$\frac{16}{3}$��
��3���ٵ�0��x��4ʱ����ͼ2�У���PM��PQ�ֱ�AD�ڵ�E��F�����ص�����Ϊ��PEF��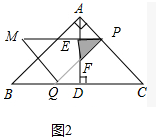
��AP=$\sqrt{2}$x��
��EF=PE=x��
��y=S��PEF=$\frac{1}{2}$•PE•EF=$\frac{1}{2}$x2��
�ڵ�4��x��$\frac{16}{3}$ʱ����ͼ3�У���PM��MQ�ֱ�AD��E��G�����ص�����Ϊ�ı���PEGQ��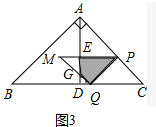
��PQ=PC=8$\sqrt{2}$-$\sqrt{2}$x��
��PM=16-2x����ME=PM-PE=16-3x��
��y=S��PMQ-S��MEG=$\frac{1}{2}$��8$\sqrt{2}$-$\sqrt{2}$x��2-$\frac{1}{2}$��16-3x��2=-$\frac{7}{2}$x2+32x-64��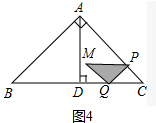
�۵�$\frac{16}{3}$��x��8ʱ����ͼ4�У����غϲ���Ϊ��PMQ��
��y=S��PMQ=$\frac{1}{2}$PQ2=$\frac{1}{2}$��8$\sqrt{2}$-$\sqrt{2}$x��2=x2-16x+64��
��������y=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2}}&{��0��x��4��}\\{-\frac{7}{2}{x}^{2}+32x-64}&{��4��x��\frac{16}{3}��}\\{{x}^{2}-16x+64}&{��\frac{16}{3}��x��8��}\end{array}\right.$��
���� ���⿼���������ۺ��⡢����ֱ�������ε����ʡ��ֶκ����������������֪ʶ������Ĺؼ�����ȷ����ͼ��ѧ��������ۣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
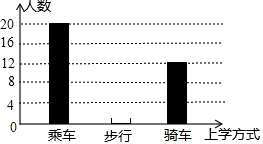 ѧϰ��ͳ��֪ʶ��С���ͱ���ͬѧ����ѧ��ʽ������һ�ε���ͳ�ƣ���ͨ���ɼ����ݺ���һ����������ͳ��ͼ����ͼ��ʾ������֪�ﳵ������ռȫ��������30%�����ͼ���ṩ����Ϣ���ɵøðಽ����ѧ����8�ˣ�
ѧϰ��ͳ��֪ʶ��С���ͱ���ͬѧ����ѧ��ʽ������һ�ε���ͳ�ƣ���ͨ���ɼ����ݺ���һ����������ͳ��ͼ����ͼ��ʾ������֪�ﳵ������ռȫ��������30%�����ͼ���ṩ����Ϣ���ɵøðಽ����ѧ����8�ˣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
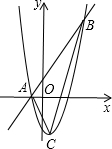 ��ͼ��������y=a��x-1��2-n��ֱ��y=2x+b�ཻ�ڵ�A��-1��0���͵�B��m��12����
��ͼ��������y=a��x-1��2-n��ֱ��y=2x+b�ཻ�ڵ�A��-1��0���͵�B��m��12�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6.22��104�� | B�� | 0.622��105�� | C�� | 6.22��105�� | D�� | 62.2��103�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��1010 | B�� | 2��109 | C�� | 20��108 | D�� | 2��107 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
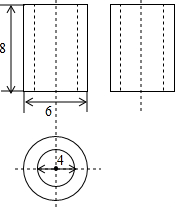 ��ͼ��ij�����������ͼ������ͼ�����ݣ��ɵøü���������Ϊ��������
��ͼ��ij�����������ͼ������ͼ�����ݣ��ɵøü���������Ϊ��������| A�� | 9�� | B�� | 40�� | C�� | 20�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��λ����31 | B�� | ������29 | C�� | ƽ������30 | D�� | ������5 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com