
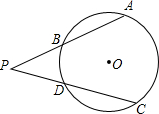
 如图,P为⊙O外一点,∠APC的两边分别交⊙O于点A,B和C,D.如果PA=PC,求证:AB=CD.
如图,P为⊙O外一点,∠APC的两边分别交⊙O于点A,B和C,D.如果PA=PC,求证:AB=CD.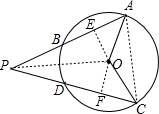
|
|


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
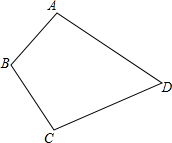 有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?查看答案和解析>>
科目:初中数学 来源: 题型:
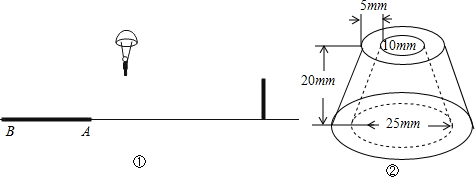
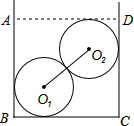 某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个
某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com