练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     

    1.计算：．+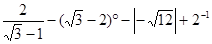

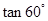
    2.如右图，P是⊙O外一点，OP垂直于弦AB于点C，交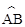于点D，连结OA、OB、AP、BP。根据以上条件，写出三个正确结论（OA=OB除外）：(6分)

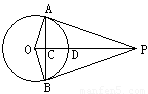
    ①              ②                ­­___ ；                       ③                           。

     

    【答案】

     

    1.

    2.

     【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    25、为了保护环境，某企业决定购买10台污水处理设备．现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如右表：经预算，该企业购买设备的资金不高于105万元．
    A型 B型
    价格（万元/台） 12 10
    处理污水量（吨/月） 240 200
    年消耗费（万元/台） 1 1
    （1）请你设计该企业有几种购买方案；
    （2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；
    （3）在第（2）问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•龙川县二模）如下图，是三个完全相同的几何体（下底面为圆面，单位：cm）．将它们拼成如右图的新几何体，则新几何体的体积为
    60π
    60π
    cm3．（计算结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•婺城区二模）初三（1）班数学兴趣小组在社会实践活动中，进行了如下的课题研究：
    用一长为18cm、宽为12cm的矩形铁皮（如右图），裁剪出一个扇形，使扇形的面积尽可能大．小组讨论后，设计了以下三种方案：
    （1）以CD为直径画弧（如图1），则截得的扇形面积为
    18π
    18π
    cm2；
    （2）以C为圆心，CD为半径画弧（如图2），则截得的扇形面积为
    36π
    36π
    cm2；
    （3）以BC为直径画弧（如图3），则截得的扇形面积为
    81
    2
    π
    81
    2
    π
    cm2；经过这三种情形的研究，小明突然受到启发，他觉得下面这一方案更佳：圆心仍在BC边上，以OC为半径画弧，切AD于E，交AB于F（如图4）．请你通过计算说明，小明的方案所截得的扇形面积更大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

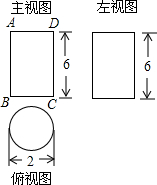    一个几何体的三视图如右图所示，
    （1）写出这个几何体的名称；
    （2）根据所示数据计算这个几何体的侧面积；
    （3）如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到CD的中点E，请你求出这个线路的最短路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

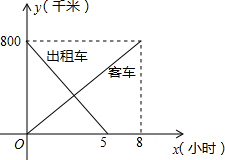    一辆客车与一辆出租车分别从甲、乙两地同时出发，相向而行．设客车离甲地的距离为y1千米，出租车离甲地的距离为y2千米，两车行驶的时间为x小时，y1、y2关于x的函数图象如右图所示：
    （1）根据图象，直接写出y1、y2关于x的函数图象关系式；
    （2）试计算：何时两车相距300千米？

    查看答案和解析>>

    同步练习册答案