
分析 (1)通过前面的等式的特点,直接得到结果,利用分式的加减证明结论;
(2)利用等式的变形计算各题;
(3)提出100后,利用(1)的结论代入求值.
解答 解:(1)$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$.
证明:$\frac{1}{n}$-$\frac{1}{n+1}$
=$\frac{n+1}{n(n+1)}-\frac{n}{n(n+1)}$
=$\frac{1}{n(n+1)}$.
(2)
①$\frac{13}{143}$-$\frac{13}{144}$
=13($\frac{1}{143}-\frac{1}{144}$)
=13×$\frac{1}{143×144}$
=$\frac{1}{1584}$;
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{99}-\frac{1}{100}$
=1-$\frac{1}{100}$
=$\frac{99}{100}$.
(3)$\frac{100}{1×2}$+$\frac{100}{2×3}$+$\frac{100}{3×4}$+…$\frac{100}{n(n+1)}$
=100($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$)
=100(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n}-\frac{1}{n+1}$)
=100(1-$\frac{1}{n+1}$)
=$\frac{100n}{n+1}$
当n=999时,原式=$\frac{999×100}{999+1}$
=$\frac{999}{10}$.
点评 本题考查了等式变形及应用.灵活运用$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$是解决本题的关键.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
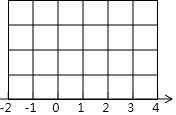 如图,每个小格的顶点叫做格点,每个小正方形边长为1,
如图,每个小格的顶点叫做格点,每个小正方形边长为1,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
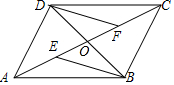 如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.
如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com