
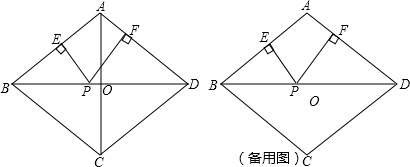
 AC=6,OB=OD,AC⊥BD,
AC=6,OB=OD,AC⊥BD, =
= =8,
=8, (16-x);
(16-x);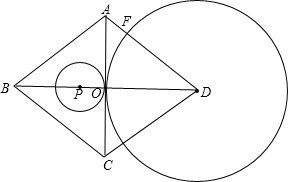
 (16-x)=16-x,
(16-x)=16-x,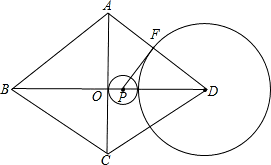
 (16-x)=16-x,
(16-x)=16-x, ;
;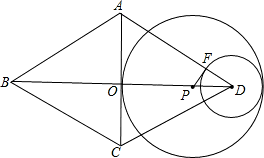
 (16-x)=16-x,
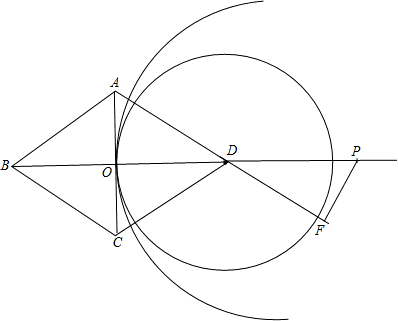
(16-x)=16-x,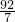 ;
;
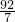 或
或 或26.
或26. (16-x),分为两种情况:①当⊙P与⊙D外切时:第一种情况,当P点在点O的左侧,PO=8-x,根据相切两圆性质得出PO+DF=PD,代入得出方程(8-x)+
(16-x),分为两种情况:①当⊙P与⊙D外切时:第一种情况,当P点在点O的左侧,PO=8-x,根据相切两圆性质得出PO+DF=PD,代入得出方程(8-x)+ (16-x)=16-x,求出x即可;第二种情况,当P点在点O的右侧,PO=x-8,根据相切两圆的性质得出PO+DF=PD,代入得出方程(x-8)+
(16-x)=16-x,求出x即可;第二种情况,当P点在点O的右侧,PO=x-8,根据相切两圆的性质得出PO+DF=PD,代入得出方程(x-8)+ (16-x)=16-x,求出方程的解即可;②当⊙P与⊙D内切时:第三种情况,PO=PB-OB=x-8,根据OP-DF═PD,得出方程(x-8)-
(16-x)=16-x,求出方程的解即可;②当⊙P与⊙D内切时:第三种情况,PO=PB-OB=x-8,根据OP-DF═PD,得出方程(x-8)- (16-x)=16-x,求出即可;第四种情况,点P在点D右侧时,PF=OD=8,则DP=10,PB=26.
(16-x)=16-x,求出即可;第四种情况,点P在点D右侧时,PF=OD=8,则DP=10,PB=26.

科目:初中数学 来源: 题型:
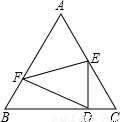
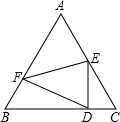 如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )
如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )A、10
| ||
B、10-5
| ||
C、5
| ||
D、20-10
|
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年最佳中考数学模拟试卷(五)(解析版) 题型:选择题
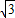 -15
-15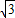
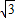 -5
-5
查看答案和解析>>
科目:初中数学 来源:2011年上海市虹口区中考数学二模试卷(解析版) 题型:选择题

 -15
-15
 -5
-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com