
【题目】请参照下面探究过程,完成所提出的问题.
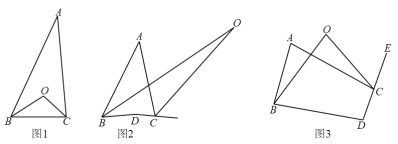
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点.
若∠A=30°,则∠BOC= ;
若∠A=α,则∠BOC= (用含α的代数式表示)
(2)如图2,在四边形ABDC中,点O是∠ABD和∠ACD外角平分线的交点,写出∠A、∠D与∠O之间的数量关系,并说明理由;
(3) 如图3,在四边形ABDC中,∠ABD和∠ACD外角的n等分线交于O,使∠ABD=n∠ABO,∠ACE=n∠ACO.直接写出∠A、∠D和∠O之间的数量关系.
【答案】(1)105°,90°+![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由三角形内角和定理可求得∠ABC+∠ACB,根据角平分线的定义可求得∠OBC+∠,在△BOC中利用三角形内角和定理可求得∠BOC;
(2)设AC与BO的交点为M,延长BD交AC于N,根据三角形内角和等于180°,四边形内角和等于360°,结合角平分线的定义即可得到∠A、∠D与∠O之间的数量关系;
(3)设AC与BO的交点为M,根据三角形内角和等于180°,四边形内角和等于360°,可得到![]() ,
,![]() ,将前式代入即可得到结论.
,将前式代入即可得到结论.
(1)∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵BO、CO是角平分线,
∴∠ABC=2∠OBC,∠ACB=2∠BCO,
∴∠OBC+∠BCO=75°,
∵∠OBC+∠BCO+∠BOC=180°,
∴∠BOC=105°;
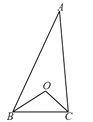
如图,在![]() 中,
中,![]() 是
是![]() 与
与![]() 的平分线
的平分线![]() 和
和![]() 的交点,
的交点,
![]()
![]()
![]()
(2)设AC与BO的交点为M,延长BD交AC于N,如图所示:
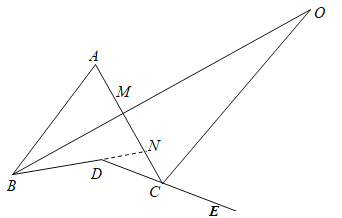
∵∠A+∠ABM+∠AMB=180°,
∴∠AMB=180°-∠A-∠ABM
∵BM是∠ABD的平分线,
∴∠ABM=![]() ∠ABD,
∠ABD,
∴∠AMB=180°-∠A-![]() ∠ABD
∠ABD
∵∠AMB=∠CMO,
∴∠CMO=180°-∠A-![]() ∠ABD,
∠ABD,
∵![]()
∴![]()
=![]()
=![]()
∴![]()
∵∠DNC是△ABN的外角,
∴∠DNC=∠A+∠ABN,
∵∠ACD与∠ACE互为邻补角,
∴∠ACD=180°-∠ACE,
∵∠BDC是△DCN的外角,
∴![]()
=![]()
=![]()
=![]()
![]()
(3)设AC与BO的交点为M,如图所示:
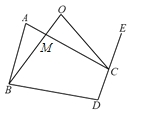
∵∠A+∠ABM+∠AMB=180°,
∴∠AMB=180°-∠A-∠ABM
∵∠AMB=∠CMO,
∴∠CMO=180°-∠A-∠ABM,
∵![]()
∴![]()
=![]()
=![]()
∴![]()
∵![]()
∴![]()
∵∠ACD+∠ACE=180°
∴∠ACD=180°-∠ACE
∵∠ABD=n∠ABO,∠ACE=n∠ACO,
∴∠D=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
![]()


科目:初中数学 来源: 题型:
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)若原方程的一根大于3,另一根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,分别以A和B为圆心,大于![]() AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
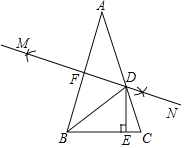
A.3B.2C.1D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
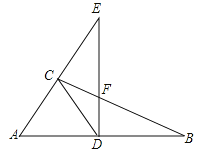
①∠DCB=∠B;②CD=![]() AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com