练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

          


     

    ＝3－＋1－6

    ＝－2－  


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    一个多边形的内角和比它的外角的和的2倍还大180°，这个多边形的边数是（  ）

    A.6   　　　  B.7    　　　 C.8   　　　 D.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：


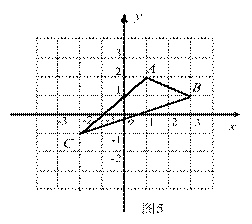
    如图，在平面直角坐标系中完成下列各题：

     

    （1）在图中作出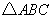关于轴对称的.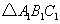                   

    （2）在x轴上画出点P，使PA+PB的值最小。

    (3)在x轴上画出点Q，使Q B1 +Q C的值最小

    查看答案和解析>>

    科目：初中数学 来源： 题型：


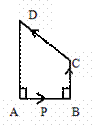
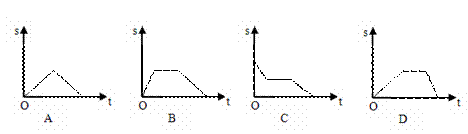
    如图，在四边形ABCD中，动点P从点A开始沿A→B→C→D的路径匀速前进到D为止.在这个过程中，△APD的面积S随时间t的变化关系用图象表示正确的是（   ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=4，则△ADE的周长是        ．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，直线L是第一、三象限的角平分线．

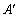    (1)由图观察易知A（0，2）关于直线l的对称点的坐标为（2，0），请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点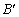、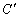的位置，并写出他们的坐标:         、              ；

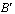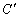    (2)结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点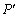的坐标为         （不必证明）；

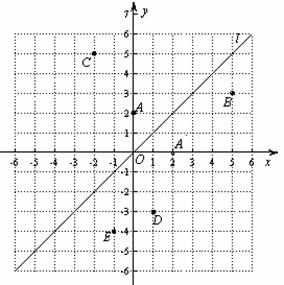    (3)已知两点D(1,-3)、E(-1,-4)，试在直线L上画出点Q，使点Q到D、E两点的距离之和最小，最小值为           ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若一元二次方程x2+x－2=0的解为x1、x2，则x1•x2的值是                 （     ）

    A．1           B．—1            C．2              D．—2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：

                                                

    查看答案和解析>>

    科目：初中数学 来源： 题型：


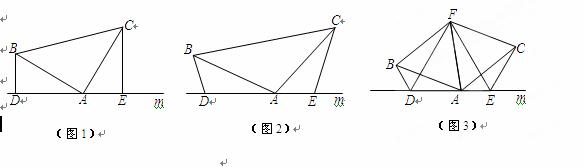
     (1)如图(1)，已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

    (2) 如图(2)，将(1)中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=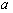,其中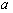为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

    (3) 拓展与应用：如图(3)，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

    查看答案和解析>>

    同步练习册答案