
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖ®Ę½µŲĆęµćA“¦ÓŠŅ»ĶųĒņ·¢ÉäĘ÷ĻņæÕÖŠ·¢ÉäĶųĒņ£¬ĶųĒņ·ÉŠŠĀ·ĻߏĒŅ»ĢõÅ×ĪļĻߣ¬ŌŚµŲĆęÉĻĀäµćĪŖB£¬ÓŠČĖŌŚÖ±ĻßABÉĻµćC£ØææµćBŅ»²ą£©ŹśÖ±ĻņÉĻ°Ś·ÅČōøÉøöĪŽøĒµÄŌ²ÖłŠĪĶ°£®ŹŌĶ¼ČĆĶųĒņĀäČėĶ°ÄŚ£¬ŅŃÖŖAB=4Ć×£¬AC=3Ć×£¬ĶųĒņ·ÉŠŠ×ī“óø߶ČOM=5Ć×£¬Ō²ÖłŠĪĶ°µÄÖ±¾¶ĪŖ0.5Ć×£¬øßĪŖ0.3Ć×£ØĶųĒņµÄĢå»żŗĶŌ²ÖłŠĪĶ°µÄŗń¶ČŗöĀŌ²»¼Ę£©£®µ±ŹśÖ±°Ś·ÅŌ²ÖłŠĪĶ°ÖĮÉŁ£Ø £©øöŹ±£¬ĶųĒņæÉŅŌĀäČėĶ°ÄŚ.

A.7B.8C.9D.10
”¾“š°ø”æB
”¾½āĪö”æ
ŅŌÅ×ĪļĻߵĶŌ³ĘÖįĪŖyÖį£¬Ė®Ę½µŲĆęĪŖxÖį£¬½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ£¬Éč½āĪöŹ½£¬½įŗĻŅŃÖŖČ·¶ØÅ×ĪļĻßÉĻµćµÄ×ų±ź£¬“śČė½āĪöŹ½Č·¶ØÅ×ĪļĻߵĽāĪöŹ½£»ÓÉŌ²Ķ°µÄÖ±¾¶£¬Ēó³öŌ²Ķ°Į½±ßŌµ×Ż×ų±źµÄÖµ£¬Č·¶ØmµÄ·¶Ī§£¬øł¾ŻmĪŖÕżÕūŹż£¬µĆ³ömµÄÖµ£¬¼“æɵƵ½µ±ĶųĒņæÉŅŌĀäČėĶ°ÄŚŹ±£¬ŹśÖ±°Ś·ÅŌ²ÖłŠĪĶ°øöŹż£®
ŅŌµćOĪŖŌµć,ABĖłŌŚÖ±ĻßĪŖxÖį½ØĮ¢Ö±½Ē×ų±źĻµ£¬
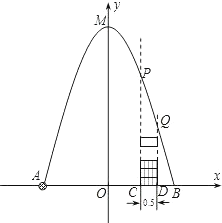
M(0,5),B(2,0),C(1,0),D(![]() ,0)
,0)
ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖ![]() £¬
£¬
Å×ĪļĻß¹żµćMŗĶµćB£¬
Ōņk=5,a=![]()
”ąÅ×ĪļĻß½āĪöŹ½ĪŖ£ŗ![]() £»
£»
µ±x=1Ź±£¬y=![]() £¬P£Ø1£¬
£¬P£Ø1£¬![]() £©
£©
µ±x=![]() Ź±£¬y=
Ź±£¬y=![]() £¬Q(
£¬Q(![]() ,
,![]() )
)
É菜ֱ°Ś·ÅŌ²ÖłŠĪĶ°møöŹ±ĶųĒņæÉŅŌĀäČėĶ°ÄŚ£¬
ÓÉĢāŅā,µĆ, ![]()
![]() m
m![]() £¬
£¬
½āµĆ£ŗ![]() m
m![]() £»
£»
”ßmĪŖÕūŹż£¬
”ąmµÄÖµĪŖ8£¬9£¬10£¬11£¬12.
”ąmµÄµ±ŹśÖ±°Ś·ÅŌ²ÖłŠĪĶ°ÖĮÉŁ8øöŹ±£¬ĶųĒņæÉŅŌĀäČėĶ°ÄŚ.
¹ŹŃ”B.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬”ĻACB£½90”ć£¬AB£½5cm£¬BC£½3cm£¬ČōµćP“ÓµćA³ö·¢£¬ŅŌĆæĆė2cmµÄĖŁ¶ČŃŲÕŪĻßA©C©B©AŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£Øt£¾0£©£®
£Ø1£©ČōµćPŌŚACÉĻ£¬ĒŅĀś×ćPA£½PBŹ±£¬Ēó³ö“ĖŹ±tµÄÖµ£»
£Ø2£©ČōµćPĒ”ŗĆŌŚ”ĻBACµÄ½ĒĘ½·ÖĻßÉĻ£¬ĒótµÄÖµ£»
£Ø3£©ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬Ö±½ÓŠ“³öµ±tĪŖŗĪÖµŹ±£¬”÷BCPĪŖµČŃüČż½ĒŠĪ£®
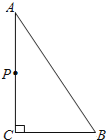
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
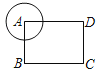
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AB£½6£¬AD£½8£¬ŅŌ¶„µćAĪŖŌ²ŠÄ×÷°ė¾¶ĪŖrµÄŌ²£¬ČōŅŖĒóĮķĶāČżøö¶„µćÖĮÉŁÓŠŅ»øöŌŚŌ²ÄŚ£¬ĒŅÖĮÉŁÓŠŅ»øöŌŚŌ²Ķā£¬ŌņrµÄȔֵ·¶Ī§ŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
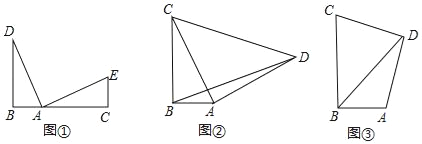
”¾ĢāÄæ”æ£Ø1£©¹Ū²ģ²ĀĻė
ČēĶ¼¢ŁµćB”¢A”¢CŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬DB”ĶBC£¬EC”ĶBCĒŅ”ĻDAE=90”ć£¬AD=AE£¬ŌņBC”¢BD”¢CEÖ®¼äµÄŹżĮæ¹ŲĻµĪŖ£»
£Ø2£©ĪŹĢā½ā¾ö
ČēĶ¼¢Ś£¬ŌŚRt”÷ABCÖŠ£¬”ĻABC=90”ć£¬CB=4£¬AB=2£¬ŅŌACĪŖÖ±½Ē±ßĻņĶā×÷µČŃüRt”÷DAC£¬Į¬½įBD£¬ĒóBDµÄ³¤£»
£Ø3£©ĶŲÕ¹ŃÓÉģ
ČēĶ¼¢Ū£¬ŌŚĖıߊĪABCDÖŠ£¬”ĻABC=”ĻADC=90”ć£¬CB=4£¬AB=2£¬DC=DA£¬ĒėÖ±½ÓŠ“³öBDµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĖ³ĒÓŠ¼×”¢ŅŅĮ½¼ŅĘĻĢŃ²ÉÕŖŌ°µÄĘĻĢŃĻśŹŪ¼ŪøńĻąĶ¬£¬ÖŠĒļĘŚ¼ä£¬Į½¼Ņ²ÉÕŖŌ°ĶĘ³öÓÅ»Ż·½°ø£¬¼×Ō°µÄÓÅ»Ż·½°øŹĒ£ŗÓĪæĶ½ųŌ°Šč¹ŗĀņĆÅʱ£¬²ÉÕŖµÄĘĻĢŃĮłÕŪÓÅ»Ż£»ŅŅŌ°µÄÓÅ»Ż·½°øŹĒ£ŗÓĪæĶ½ųŌ°²»Šč¹ŗĀņĆÅʱ£¬²ÉÕŖŌ°µÄĘĻĢŃ°“ŹŪ¼Ūø¶æī”£ÓÅ»ŻĘŚ¼ä£¬ÉčÓĪæĶµÄĘĻĢŃ²ÉÕŖĮæĪŖ![]() £ØĒ§æĖ£©£¬ŌŚ¼×Ō°ĖłŠč×Ü·ŃÓĆĪŖ
£ØĒ§æĖ£©£¬ŌŚ¼×Ō°ĖłŠč×Ü·ŃÓĆĪŖ![]() ¼×£ØŌŖ£©£¬ŌŚŅŅŌ°ĖłŠč×Ü·ŃÓĆĪŖ
¼×£ØŌŖ£©£¬ŌŚŅŅŌ°ĖłŠč×Ü·ŃÓĆĪŖ![]() ŅŅ£ØŌŖ£©£¬
ŅŅ£ØŌŖ£©£¬![]() ¼×£¬
¼×£¬![]() ŅŅÓė
ŅŅÓė![]() Ö®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
Ö®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
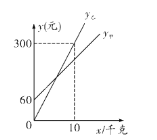
£Ø1£©Ēó![]() ¼×£¬
¼×£¬![]() ŅŅÓė
ŅŅÓė![]() µÄŗÆŹż±ķ“ļŹ½£»
µÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ŌŚÖŠĒļĘŚ¼ä£¬ĄīÄČŅ»¼ŅČżæŚ×¼±øČ„ĘĻĢŃŌ°²ÉÕŖĘĻĢŃ£¬²ÉÕŖµÄĘĻĢŃŗĻŌŚŅ»ĘšÖ§ø¶·ŃÓĆ£¬ŌņĄīÄČŅ»¼ŅӦєŌńÄļŅĘĻĢŃŌ°øü»®Ėć£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ![]() µÄÖ±¾¶
µÄÖ±¾¶![]() £¬
£¬![]() ”¢
”¢![]() ĪŖ
ĪŖ![]() µÄČżµČ·Öµć£¬
µÄČżµČ·Öµć£¬![]() ”¢
”¢![]() ĪŖ
ĪŖ![]() ÉĻĮ½µć£¬ĒŅ
ÉĻĮ½µć£¬ĒŅ![]()
![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ”ĒųæŖÕ¹ĮĖ”°ŠŠ³µ°²Č«£¬·½±ć¾ÓĆń”±µÄ»ī¶Æ£¬¶ŌµŲĻĀ³µæā×÷ĮĖøĽų£®ČēĶ¼£¬ÕāŠ”ĒųŌµŲĻĀ³µæāµÄČėæŚ“¦ÓŠŠ±ĘĀAC³¤ĪŖ13Ć×£¬ĖüµÄĘĀ¶ČĪŖi£½1£ŗ2.4£¬AB”ĶBC£¬ĪŖĮĖ¾ÓĆńŠŠ³µ°²Č«£¬ĻÖ½«Š±ĘĀµÄĘĀ½ĒøÄĪŖ13”ć£¬¼“”ĻADC£½13”ć£Ø“ĖŹ±µćB”¢C”¢DŌŚĶ¬Ņ»Ö±ĻßÉĻ£©£®
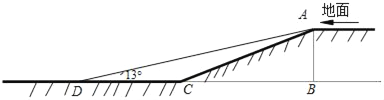
£Ø1£©ĒóÕāøö³µæāµÄø߶ČAB£»
£Ø2£©ĒóŠ±ĘĀøĽųŗóµÄĘšµćDÓėŌĘšµćCµÄ¾ąĄė£Ø½į¹ū¾«Č·µ½0.1Ć×£©£®
£Ø²Īæ¼Źż¾Ż£ŗsin13”ć”Ö0.225£¬cos13”ć”Ö0.974£¬tan13”ć”Ö0.231£¬cot13”ć”Ö4.331£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
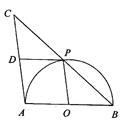
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ°ėŌ²OµÄÖ±¾¶£¬µćPŹĒ°ėŌ²ÉĻ²»ÓėµćA£¬BÖŲŗĻµÄŅ»øö¶Æµć£¬ŃÓ³¤BPµ½µćC£¬Ź¹PC£½PB£¬DŹĒACµÄÖŠµć£¬Į¬½ÓPD£¬PO£®
£Ø1£©ĒóÖ¤£ŗ”÷CDP”Õ”÷POB£»
£Ø2£©ĢīæÕ£ŗ
¢ŁČōAB£½4£¬ŌņĖıߊĪAOPDµÄ×ī“óĆ껿ĪŖ_______£¬“ĖŹ±BD=_______£»
¢ŚĮ¬½ÓOD£¬µ±”ĻPBAµÄ¶ČŹżĪŖ________Ź±£¬ĖıߊĪBPDOŹĒĮāŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćAŌŚxÖįÕż°ėÖįÉĻ£¬µćBŌŚyÖįÕż°ėÖįÉĻ£¬OĪŖ×ų±źŌµć£¬OA£½OB£½1£¬¹żµćO×÷OM1”ĶABÓŚµćM1£»¹żµćM1×÷M1A1”ĶOAÓŚµćA1£ŗ¹żµćA1×÷A1M2”ĶABÓŚµćM2£»¹żµćM2×÷M2A2”ĶOAÓŚµćA2”ŅŌ“ĖĄąĶĘ£¬µćM2019µÄ×ų±źĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com