练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一个三角形的三个内角的度数比是1 ∶6 ∶5 ，最大的一个内角是__________度，按角分，它是一个________角三角形.

    【答案】 90 直角

    【解析】设这个三角形的最小内角为x，则另外两个角分别为6x、5x，根据三角形的内角和定理可得x+6x+5x=180，解得x=15，所以这个三角形的最大内角为15×6=90°，这个三角形是直角三角形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】“三次投掷一枚硬币，三次正面朝上”这一事件是（ ）
    A.必然事件
    B.随机事件
    C.不可能事件
    D.确定事件

    查看答案和解析>>

    科目：初中数学 来源： 题型：

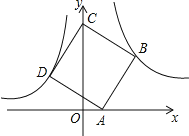
    【题目】如图，点B（3，3）在双曲线y=（x＞0）上，点D在双曲线y=﹣（x＜0）上，点A和点C分别在x轴、y轴的正半轴上，且点A、B、C构成的四边形为正方形

    （1）求k的值；

    （2）求点A的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC是⊙O的内接三角形，且∠BOC=80°则∠BAC=______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】写出一个解为1和-2的一元二次方程______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上，OC=8，OE=17，抛物线y=x2﹣3x+m与y轴相交于点A，抛物线的对称轴与x轴相交于点B，与CD交于点K．

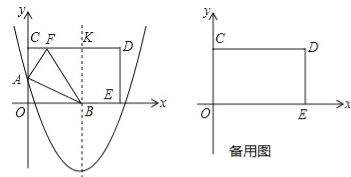
    （1）将矩形OCDE沿AB折叠，点O恰好落在边CD上的点F处．

    ①点B的坐标为（ 、 ），BK的长是 ，CK的长是 ；

    ②求点F的坐标；

    ③请直接写出抛物线的函数表达式；

    （2）将矩形OCDE沿着经过点E的直线折叠，点O恰好落在边CD上的点G处，连接OG，折痕与OG相交于点H，点M是线段EH上的一个动点（不与点H重合），连接MG，MO，过点G作GP⊥OM于点P，交EH于点N，连接ON，点M从点E开始沿线段EH向点H运动，至与点N重合时停止，△MOG和△NOG的面积分别表示为S1和S2，在点M的运动过程中，S1S2（即S1与S2的积）的值是否发生变化？若变化，请直接写出变化范围；若不变，请直接写出这个值．

    温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△AOB中，∠AOB=90°，OA在x轴上，OB在y轴上，点A，B的坐标分别为（，0），（0，1），把Rt△AOB沿着AB对折得到Rt△AO′B，则点O′的坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一时刻，身高1.6m的小强的影长是1.2m，旗杆的影长是15m，则旗杆高为（ ）

    A. 16m B. 18m C. 20m D. 22m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

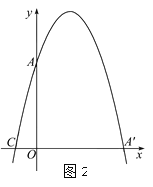
    【题目】在平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别是（0，4）、（﹣1，0），将此平行四边形绕点O顺时针旋转90°，得到平行四边形A′B′OC′．

    （1）若抛物线经过点C、A、A′，求此抛物线的解析式；

    （2）点M时第一象限内抛物线上的一动点，问：当点M在何处时，△AMA′的面积最大？最大面积是多少？并求出此时M的坐标；

    （3）若P为抛物线上一动点，N为x轴上的一动点，点Q坐标为（1，0），当P、N、B、Q构成平行四边形时，求点P的坐标，当这个平行四边形为矩形时，求点N的坐标．

    查看答案和解析>>

    同步练习册答案