
| A. | -4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | 4 |
科目:初中数学 来源: 题型:解答题
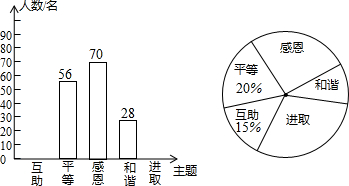
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
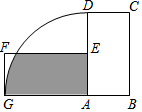 如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为$\widehat{DG}$,若AB=1,BC=2,则阴影部分的面积为( )
如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为$\widehat{DG}$,若AB=1,BC=2,则阴影部分的面积为( )| A. | $\frac{π}{3}$+$\frac{\sqrt{3}}{2}$ | B. | 1+$\frac{\sqrt{3}}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | ±2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 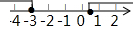 | C. |  | D. | 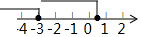 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
某公司销售一种服装,进价120元/件,售价200元/件,公司对大量购买有优惠政策,凡是一次性购买20件以上的,每多买一件,售价就降低1元.设顾客购买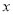 (件)时公司的利润为
(件)时公司的利润为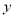 (元).
(元).
(1)当一次性购买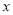 件
件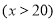 时,
时,
①售价为 元/件;
②求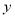 (元)与
(元)与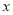 (件)之间的函数表达式
(件)之间的函数表达式
?在此优惠政策下,顾客购买多少件时公司能够获得最大利润?
(2) 设售价为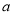 元/件,求
元/件,求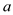 在什么范围内才能保证公司每次卖的越多,利润也越多.
在什么范围内才能保证公司每次卖的越多,利润也越多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com