
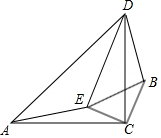
 如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,
如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,分析 (1)根据△ACD和△BCE都是等腰直角三角形、∠ACD=∠BCE=90°,即可得出AC=DC、EC=BC,再由角的计算即可得出∠ACE=∠DCB,利用全等三角形的判定定理SAS即可证出△ACE≌△DCB,进而可得出AE=DB.延长AE,交CD于点H,交BD于点F,根据角的计算即可得出∠DFH=∠ACD=90°,从而找出AE⊥BD;
(2)根据△BCE是等腰直角三角形即可得出∠CEB=∠CBE=45°,结合∠AED=135°、∠AEC=α即可找出∠DEB=180°-α,由(1)△ACE≌△DCB可得出∠DBC=∠AEC=α,进而得出∠DBE=α-45°,再根据三角形内角和定理即可得出∠EDB=45°,分∠DEB=∠DBE、∠DEB=∠EDB以及∠DBE=∠EDB三种情况考虑△BDE为等腰三角形,代入数据求出α值,此题得解.
解答 解:(1)AE=BD且AE⊥BD,理由如下:
∵△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,
∴AC=DC,EC=BC.
∵∠ACD=∠ACE+∠ECD=90°,∠BCE=∠DCB+∠ECD=90°,
∴∠ACE=∠DCB.
在△ACE和△DCB中,$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{EC=BC}\end{array}\right.$,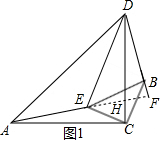
∴△ACE≌△DCB(SAS),
∴AE=DB,∠CAE=∠CDB.
延长AE,交CD于点H,交BD于点F,如图1所示.
∵∠AHD=∠CHF=∠CDB+∠DFH,∠AHD=∠CAE+∠ACD,
∴∠DFH=∠ACD=90°,
∴AE⊥BD.
(2)∵△BCE是等腰直角三角形,∠BCE=90°,
∴∠CEB=∠CBE=45°,
∵∠AED=135°,∠AEC=α,
∴∠DEB=360°-∠AED-∠CEB-∠AEC=360°-135°-45°-α=180°-α.
∵△ACE≌△DCB,
∴∠DBC=∠AEC=α,
∴∠DBE=α-45°.
在△DBE中,∠EDB=180°-∠DEB-∠DBE=180°-(180°-α)-(α-45°)=45°.
△BDE为等腰三角形分三种情况:
①∠DEB=∠DBE,即180°-α=α-45°,
∴α=112.5°;
②∠DEB=∠EDB,即180°-α=45°,
∴α=135°;
③∠DBE=∠EDB,即α-45°=45°,
∴α=90°.
综上所述:当△BDE为等腰三角形时,α的度数为112.5°、135°或90°.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形以及三角形内角和定理,熟练掌握全等三角形的判定与性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 两个有理数的和不一定大于每一个加数 | |
| B. | 任何有理数的绝对值都不小于0 | |
| C. | 最小的非负整数是0 | |
| D. | 一个数的绝对值等于它本身,则这个数是正数. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
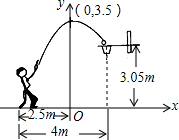 宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com