
【题目】春华中学为了解九年级学生的身高情况,随机抽测50名学生的身高后,所得部分资料如下(身高单位:![]() ,测量时精确到
,测量时精确到![]() ):
):
身高 | 148 | 151 | 154 | 155 | 157 | 158 | 160 | 161 | 162 | 164 |
人数 | 1 | 1 | 2 | 1 | 2 | 3 | 4 | 3 | 4 | 5 |
身高 | 165 | 166 | 167 | 168 | 170 | 171 | 173 | 175 | 177 | 179 |
人数 | 2 | 3 | 6 | 1 | 4 | 2 | 3 | 1 | 1 | 1 |
若将数据分成8组,取组距为![]() ,相应的频率分布表(部分)是:
,相应的频率分布表(部分)是:
分组 | 频数 | 频率 |
147.5~151.5 | 2 | 0.04 |
151.5~155.5 | 3 | 0.06 |
155.5~159.5 | 5 | 0.10 |
159.5~163.5 | 11 | 0.22 |
163.5~167.5 | ________ | ________ |
167.5~171.5 | 7 | 0.14 |
171.5~175.5 | 4 | 0.08 |
175.5~179.5 | 2 | 0.04 |
合计 | 50 | 1.00 |
请回答下列问题:
(1)样本数据中,学生身高的众数、中位数各是多少?
(2)填写频率分布表中未完成的部分;
(3)若该校九年级共有850名学生,请你估计该年级学生身高在![]() 及以上的人数.
及以上的人数.
【答案】(1)众数是![]() ,中位数是
,中位数是![]() ;(2)163.5~167.5频数16,频率为0.32.(3)该年级学生身高在
;(2)163.5~167.5频数16,频率为0.32.(3)该年级学生身高在![]() 及以上的人数为102人.
及以上的人数为102人.
【解析】
(1)根据众数的定义以及中位数的定义得出众数、中位数即可;
(2)利用图表中不同身高的人数分布情况求出未知的频数和频率即可;
(3)利用样本中身高在172cm及以上学生的频率估计总体学生身高在172cm及以上的人数即可.
解:(1)∵图表中167cm的人数最多为6人,
∴众数为:167cm;
∵共50人,中位数应该是第25和第26人的平均数,
∴第25和第26人的平均数为:![]() =164(cm)
=164(cm)
答:众数是![]() ,中位数是
,中位数是![]() ;
;
(2)163.5~167.5范围内的人数为:5+2+3+6=16(人),
163.5~167.5范围内的频率为:![]() =0.32,
=0.32,
∴163.5~167.5频数16,频率为0.32;
(3)![]() ,
,![]() 人
人
答:则该年级学生身高在![]() 及以上的人数为102人.
及以上的人数为102人.
故答案为:(1)众数是![]() ,中位数是
,中位数是![]() ;(2)163.5~167.5频数16,频率为0.32.(3)该年级学生身高在
;(2)163.5~167.5频数16,频率为0.32.(3)该年级学生身高在![]() 及以上的人数为102人.
及以上的人数为102人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如果一个正整数m能写成m=a2﹣b2(a、b均为正整数,且a≠b),我们称这个数为“平方差数”,则a、b为m的一个平方差分解,规定:F(m)=![]() .
.
例如:8=8×1=4×2,由8=a2﹣b2=(a+b)(a﹣b),可得![]() 或
或![]() .因为a、b为正整数,解得
.因为a、b为正整数,解得![]() ,所以F(8)=
,所以F(8)=![]() .又例如:48=132﹣112=82﹣42=72﹣12,所以F(48)=
.又例如:48=132﹣112=82﹣42=72﹣12,所以F(48)=![]() 或
或![]() 或
或![]() .
.
(1)判断:6 平方差数(填“是“或“不是“),并求F(45)的值;
(2)若s是一个三位数,t是一个两位数,s=100x+5,t=10y+x(1≤x≤4,1≤y≤9,x、y是整数),且满足s+t是11的倍数,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
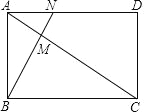
【题目】如图,已知矩形 ABCD 中,AB=1,BC=![]() ,点 M 在 AC 上,且 AM=
,点 M 在 AC 上,且 AM=![]() AC,连接并延长 BM 交 AD 于点 N.
AC,连接并延长 BM 交 AD 于点 N.
(1)求证:△ABC∽△AMB;
(2)求 MN 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
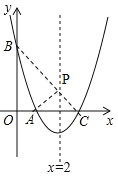
【题目】如图,抛物线![]() 交x轴于点
交x轴于点![]() ,交y轴于点B,对称轴是直线
,交y轴于点B,对称轴是直线![]() .
.
(1)求抛物线的解析式;
(2)P是抛物线对称轴上的一个动点,是否存在点P,使![]() 的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交x轴的负半轴于点
交x轴的负半轴于点![]() ,交x轴的正半轴于点
,交x轴的正半轴于点![]() ,交y轴的负半轴于点
,交y轴的负半轴于点![]() ,且
,且![]() .
.
(1)如图,求a的值
(2)如图,点![]() 在第一象限的抛物线上,连接
在第一象限的抛物线上,连接![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(3)如图,在(2)的条件下,点![]() 在第一象限的抛物线上,过点
在第一象限的抛物线上,过点![]() 作
作![]() 的垂线,交x轴于点
的垂线,交x轴于点![]() ,点
,点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() .若EP=OG,∠PEF+∠G=45°,求点
.若EP=OG,∠PEF+∠G=45°,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
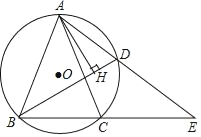
【题目】如图,△ABC内接于⊙O,BC=2,AB=AC,点D为![]() 上的动点,且cos∠ABC=
上的动点,且cos∠ABC=![]() .
.
(1)求AB的长度;
(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由;
(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
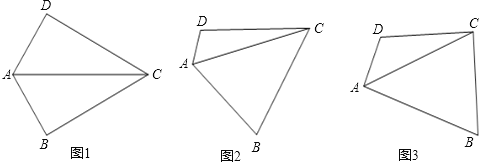
【题目】在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.
(1)问题发现:如图1,若∠DAB=120°,且∠B=90°,求证:AD+AB=AC;
(2)思考探究:如图2,若将(1)中的条件“∠B=90°”去掉,则(1)中的结论是否仍成立?请说明理由;
(3)拓展应用:如图3,若∠DAB=90°,AD=2,AB=3,求线段AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
(1)当![]() 时,求AE的长;
时,求AE的长;
(2)当AF取得最小值时,求折痕EF的长;
(3)连接CF,当![]() 是以CG为底的等腰三角形时,直接写出BG的长.
是以CG为底的等腰三角形时,直接写出BG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com