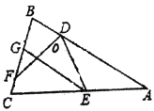
【题目】如图，在
中，
，
、
分别为
、
上的点，
、
的平分线分别交
于点
、
，
．若
，则
的度数为__________．
【答案】70°
【解析】
根据等腰三角形性质得∠B=∠C，根据角平分线定义和平行线性质得∠GED=∠CEG=40°，根据四边形内角和性质得∠BDE=360°-∠B-∠BGE-∠DEG=360°-70°-110°-40°．
因为AB=AC
所以∠B=∠C
因为DF,EG分别是∠BDE和∠CED的平分线
所以∠DEC=
∠BDE
∠CEG=∠DEG
因为EG∥AB，∠BGE=110°
所以∠B=180°-∠BGE=180°-110°=70°
所以∠A=180°-2∠B=180°-140°=40°
所以∠CEG=∠A=40°
所以∠GED=∠CEG=40°
所以∠BDE=360°-∠B-∠BGE-∠DEG=360°-70°-110°-40°=140°
所以∠BDF=∠BDE=70°
故答案为：70°．
阅读快车系列答案科目：初中数学 来源： 题型：
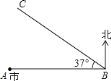
【题目】某日上午
点钟，
市气象局测得在城市正东方向
处
点有一台风中心正在以
千米/时的速度沿西偏北
的
方向迅速移动（如图所示）．据资料表明，在距离台风中心
范围内为严重影响区域（假定台风中心移动方向不变，影响力不变）．（参考数据：
，
）．
（1）市会不会受这次台风的严重影响，为什么；
（2）如果市会受严重影响，那么这次台风对市严重影响多长时间？
（3）市规定台风严重影响前一小时向市民发出预警警报．如果市会受这次台风严重影响，那么市应在几点钟发出预警警报？
查看答案和解析>>
科目：初中数学 来源： 题型：
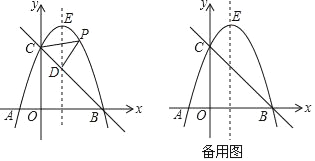
【题目】如图，在平面直角坐标系中，抛物线y＝ax2+2x+c与x轴交A（﹣1，0），B两点，与y轴交于点C（0，3），抛物线的顶点为点E．
(1)求抛物线的解析式；
(2)经过B，C两点的直线交抛物线的对称轴于点D，点P为直线BC上方抛物线上的一个动点，当点P运动到点E时，求△PCD的面积；
(3)点N在抛物线对称轴上，点M在x轴上，是否存在这样的点M与点N，使以M，N，C，B为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标（不写求解过程）；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
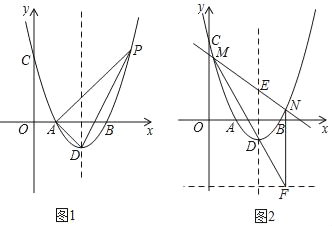
【题目】在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于A（1，0），B（3，0），与y轴交于C（0，3），抛物线顶点为D点．
(1)求此抛物线解析式；
(2)如图1，点P为抛物线上的一个动点，且在对称轴右侧，若△ADP面积为3，求点P的坐标；
(3)在(2)的条件下，PA交对称轴于点E，如图2，过E点的任一条直线与抛物线交于M，N两点，直线MD交直线y＝﹣3于点F，连结NF，求证：NF∥y轴．
查看答案和解析>>
科目：初中数学 来源： 题型：
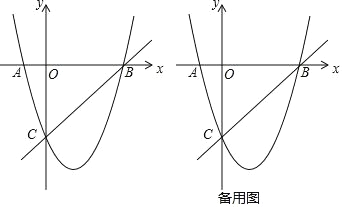
【题目】在平面直角坐标系中，二次函数的图象交坐标轴于 A（﹣1，0），B（4，0），C
（0，﹣4）三点，点 P 是直线 BC 下方抛物线上一动点．
（1） 求这个二次函数的解析式；
（2） 是否存在点 P，使△POC 是以 OC 为底边的等腰三角形？若存在，求出 P 点坐标；若不存在，请说明理由；
（3） 在抛物线上是否存在点 D（与点 A 不重合）使得 S△DBC＝S△ABC，若存在，求出点 D的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在每个小正方形的边长都是
的正方形网格中，
的三个顶点都在小正方形的格点上．将绕点
旋转
得到
（点
、
分别与点
、
对应），连接
，
．
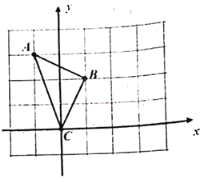
（1）请直接在网格中补全图形；
（2）四边形
的周长是________________（长度单位）
（3）直接写出四边形是何种特殊的四边形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
