
 如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(10,0)、C的坐标为(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是以OD为腰的等腰三角形时,点P的坐标为(2,4)或(8,4)或(3,4).
如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(10,0)、C的坐标为(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是以OD为腰的等腰三角形时,点P的坐标为(2,4)或(8,4)或(3,4). 分析 根据点A、C的坐标求出OA、OC,再根据线段中点的定义求出OD=5,过点P作PE⊥x轴于E,根据已知点P(3,4)判断出OP=OD,再根据PD=OD利用勾股定理列式求出DE的长,然后分点E在点D的左边与右边两种情况求出OE,然后写出点P的坐标即可.
解答 解:∵A(10,0),C(0,4)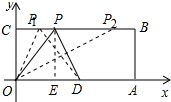
∴OA=10,OC=4,
∵点D是OA的中点,
∴OD=$\frac{1}{2}$OA=$\frac{1}{2}$×10=5,
过点P作PE⊥x轴于E,
则PE=OC=4,
∵P(3,4),
∴OP=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴此时,OP=OD,
当PD=OD时,
由勾股定理得,DE=$\sqrt{P{D}^{2}-P{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
若点E在点D的左边,OE=5-3=2,
此时,点P的坐标为(2,4),
若点E在点D的右边,则OE=5+3=8,
此时,点P的坐标为(8,4),
当PO=OD时,OE=$\sqrt{O{P}^{2}-P{E}^{2}}$=3,
∴此时,点P的坐标为(3,4),
综上所述,其余的点P的坐标为(2,4)或(8,4)或(3,4).
故答案为:(2,4)或(8,4)或(3,4).
点评 本题考查了矩形的性质,坐标与图形性质,等腰三角形的性质,勾股定理,难点在于要分两种情况写出点P的坐标.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
| 售价(元/千克) | 销售数量(kg) | |
| 前两天 | ①$\frac{3000}{x}•(1+40%)$ | 150 |
| 第三天 | ②$\frac{3000}{x}•(1-20%)$ | ③x-150 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ABC=2∠C,BE平分∠ABC,交AC于点E,过点E分别作ED⊥BC,EF⊥AB,分别交BC,AB于点D,F,若EF=6,BE=10,CD=8,则△CDE的周长为24.
如图,在△ABC中,∠ABC=2∠C,BE平分∠ABC,交AC于点E,过点E分别作ED⊥BC,EF⊥AB,分别交BC,AB于点D,F,若EF=6,BE=10,CD=8,则△CDE的周长为24.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长为1的菱形ABCD中,∠DAB=60°,以对角线AC为边作第2个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第3个菱形AEGH使∠HAE=60°…,则第3个菱形的边长是3,按此规律所作第n个菱形的边长是($\sqrt{3}$)n-1.
如图,边长为1的菱形ABCD中,∠DAB=60°,以对角线AC为边作第2个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第3个菱形AEGH使∠HAE=60°…,则第3个菱形的边长是3,按此规律所作第n个菱形的边长是($\sqrt{3}$)n-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com