
”¾ĢāÄæ”æijŅʶÆĶ؊Ź«Ė¾ĶĘ³öĮĖČēĻĀĮ½ÖÖŅĘ¶Æµē»°¼Ę·Ń·½Ź½£¬
ŌĀŹ¹ÓĆ·Ń/ŌŖ | Ö÷½ŠĻŽ¶ØŹ±¼ä/·ÖÖÓ | Ö÷½Š³¬Ź±·Ń£ØŌŖ/·ÖÖÓ£© | |
·½Ź½Ņ» | 30 | 600 | 0.20 |
·½Ź½¶ž | 50 | 600 | 0.25 |
ĖµĆ÷£ŗŌĀŹ¹ÓĆ·Ń¹Ģ¶ØŹÕČ”£¬Ö÷½Š²»³¬¹żĻŽ¶ØŹ±¼ä²»ŌŁŹÕ·Ń£¬³¬¹ż²æ·Ö¼ÓŹÕ³¬Ź±·Ń£®ĄżČē£¬·½Ź½Ņ»ĆæŌĀ¹Ģ¶Ø½»·Ń30ŌŖ£¬µ±Ö÷½Š¼ĘŹ±²»³¬¹ż300·ÖÖÓ²»ŌŁ¶īĶāŹÕ·Ń£¬³¬¹ż300·ÖÖÓŹ±£¬³¬¹ż²æ·ÖĆæ·ÖÖÓ¼ÓŹÕ0.20ŌŖ£Ø²»×ć1·ÖÖÓ°“1·ÖÖÓ¼ĘĖć£©
£Ø1£©Ēėøł¾ŻĢāŅāĶź³ÉČē±ķµÄĢīæÕ£»
ŌĀÖ÷½ŠŹ±¼ä500·ÖÖÓ | ŌĀÖ÷½ŠŹ±¼ä800·ÖÖÓ | |
·½Ź½Ņ»ŹÕ·Ń/ŌŖ | ”” ”” | 130 |
·½Ź½¶žŹÕ·Ń/ŌŖ | 50 | ”” ”” |
£Ø2£©ÉčijŌĀÖ÷½ŠŹ±¼äĪŖt£Ø·ÖÖÓ£©£¬·½Ź½Ņ»”¢·½Ź½¶žĮ½ÖÖ¼Ę·Ń·½Ź½µÄ·ŃÓĆ·Ö±šĪŖy1£ØŌŖ£©£¬y2£ØŌŖ£©£¬·Ö±šŠ“³öĮ½ÖÖ¼Ę·Ń·½Ź½ÖŠÖ÷½ŠŹ±¼ät£Ø·ÖÖÓ£©Óė·ŃÓĆĪŖy1£ØŌŖ£©£¬y2£ØŌŖ£©µÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©Ēė¼ĘĖćĖµĆ÷Ń”ŌńÄÄÖÖ¼Ę·Ń·½Ź½øüŹ”Ē®£®
”¾“š°ø”æ£Ø1£©70£»100£»£Ø2£©Ļź¼ū½āĪö£»£Ø3£©µ±0”Üt”Ü400Ź±·½Ź½Ņ»Ź”Ē®£»µ±400£¼t”Ü1400Ź±£¬·½Ź½¶žŹ”Ē®£¬µ±t£¾1400Ź±£¬·½Ź½Ņ»Ź”Ē®£¬µ±ĪŖ400·ÖÖÓ”¢1400·ÖÖÓŹ±£¬Į½ÖÖ·½Ź½·ŃÓĆĻąĶ¬£®
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāµĆ³ö±ķÖŠŹż¾Ż¼“æÉ£»
£Ø2£©øł¾Ż·Ö¶Ī¼Ę·ŃµÄ·ŃÓĆ¾ĶæÉŅŌµĆ³öø÷øöŹ±¶Īø÷ÖÖ²»Ķ¬µÄø¶·Ń·½·Ø¾ĶæÉŅŌµĆ³ö½įĀŪ£»
£Ø3£©·Ö±šĒó³ö¼øÖÖĒéæöĻĀŹ±xµÄȔֵ·¶Ī§£¬øł¾ŻxµÄȔֵ·¶Ī§¼“æÉŃ”Ōń¼Ę·Ń·½Ź½£®
½ā£ŗ£Ø1£©ÓÉĢāŅāæÉµĆ£ŗŌĀÖ÷½ŠŹ±¼ä500·ÖÖÓŹ±£¬·½Ź½Ņ»ŹÕ·ŃĪŖ70ŌŖ£»ŌĀÖ÷½ŠŹ±¼ä800·ÖÖÓŹ±£¬·½Ź½¶žŹÕ·ŃĪŖ100ŌŖ£¬
¹Ź“š°øĪŖ£ŗ70£»100£»
£Ø2£©ÓÉĢāŅāæÉµĆ£ŗy1£ØŌŖ£©µÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ
![]() £»
£»
y2£ØŌŖ£©µÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ
![]() £»
£»
£Ø3£©¢Łµ±0”Üt”Ü300Ź±·½Ź½Ņ»øüŹ”Ē®£»
¢Śµ±300£¼t”Ü600Ź±£¬ČōĮ½ÖÖ·½Ź½·ŃÓĆĻąĶ¬£¬Ōņµ±0.2t©30£½50£¬
½āµĆ£ŗt£½400£¬
¼“µ±t£½400£¬Į½ÖÖ·½Ź½·ŃÓĆĻąĶ¬£¬
µ±300£¼t”Ü400Ź±·½Ź½Ņ»Ź”Ē®£¬
µ±400£¼t”Ü600Ź±£¬·½Ź½¶žŹ”Ē®£»
¢Ūµ±t£¾600Ź±£¬ČōĮ½ÖÖ·½Ź½·ŃÓĆĻąĶ¬£¬Ōņµ±0.2t©30£½0.25t©100£¬
½āµĆ£ŗt£½1400£¬
¼“µ±t£½1400£¬Į½ÖÖ·½Ź½·ŃÓĆĻąĶ¬£¬µ±600£¼t”Ü1400Ź±·½Ź½¶žŹ”Ē®£¬
µ±t£¾1400Ź±£¬·½Ź½Ņ»Ź”Ē®£»
×ŪÉĻĖłŹö£¬µ±0”Üt”Ü400Ź±·½Ź½Ņ»Ź”Ē®£»µ±400£¼t”Ü1400Ź±£¬·½Ź½¶žŹ”Ē®£¬µ±t£¾1400Ź±£¬·½Ź½Ņ»Ź”Ē®£¬µ±ĪŖ400·ÖÖÓ”¢1400·ÖÖÓŹ±£¬Į½ÖÖ·½Ź½·ŃÓĆĻąĶ¬£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹµŃéÖ¤Ć÷£¬Ę½Ćę¾µ·“Éä¹āĻߵĹęĀÉŹĒ£ŗÕÕÉäµ½Ę½Ćę¾µÉĻµÄ¹āĻßŗĶ±»·“Éä³öµÄ¹āĻßÓėĘ½Ćę¾µĖł¼ŠµÄČń½ĒĻąµČ£®
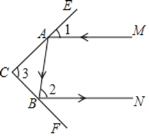
ČēĶ¼£¬Ņ»Źų¹āĻßMAÕÕÉäµ½Ę½Ćę¾µCEÉĻ£¬±»CE·“Éäµ½Ę½Ćę¾µCFÉĻ£¬ÓÖ±»CF·“É䣮ŅŃÖŖ±»CF·“Éä³öµÄ¹āĻßBNÓė¹āĻßMAĘ½ŠŠ£®Čō”Ļ1=35”ć£¬Ōņ”Ļ2= £¬”Ļ3= £»Čō”Ļ1=50”ć£¬”Ļ3= £®
£Ø2£©ÓÉ£Ø1£©²ĀĻė£ŗµ±Į½Ę½Ćę¾µCE£¬CFµÄ¼Š½Ē”Ļ3ĪŖ¶ąÉŁ¶ČŹ±£¬æÉŅŌŹ¹ČĪŗĪÉäµ½Ę½Ćę¾µCEÉĻµÄ¹āĻßMA£¬¾¹żĘ½Ćę¾µCE£¬CFµÄĮ½“Ī·“Éäŗó£¬ČėÉä¹āĻßMAÓė·“Éä¹āĻßBNĘ½ŠŠ£¬ĒėÄ抓³öĶĘĄķ¹ż³Ģ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹¤µŲŅņµĄĀ·½ØÉčŠčŅŖæŖĶŚĶĮŹÆ·½£¬¼Ę»®Ć抔Ź±ĶŚ¾ņĶĮŹÆ·½540m3£¬ĻÖ¾ö¶ØĻņij“óŠĶ»śŠµ×āĮŽ¹«Ė¾×āÓĆ¼×”¢ŅŅĮ½ÖÖŠĶŗŵÄĶŚ¾ņ»śĄ“Ķź³ÉÕāĻī¹¤×÷£¬×āĮŽ¹«Ė¾Ģį¹©µÄĶŚ¾ņ»śÓŠ¹ŲŠÅĻ¢Čē±ķ£ŗ
×ā½š£Øµ„Ī»£ŗŌŖ/ĢØŹ±£© | ĶŚ¾ņĶĮŹÆ·½Įæ£Øµ„Ī»£ŗm3/ĢØŹ±£© | |
¼×ŠĶ»ś | 100 | 60 |
ŅŅŠĶ»ś | 120 | 80 |
£Ø1£©Čō×āÓĆ¼×”¢ŅŅĮ½ÖÖŠĶŗŵÄĶŚ¾ņ»ś¹²8ĢØ£¬Ē”ŗĆĶź³ÉĆ抔Ź±µÄĶŚ¾ņĮ棬Ōņ¼×”¢ŅŅĮ½ÖÖŠĶµÄĶŚ¾ņ»śø÷Šč¶ąÉŁĢØ£æ
£Ø2£©Čē¹ūĆ抔Ź±Ö§ø¶µÄ×ā½š²»³¬¹ż850ŌŖ£¬ÓÖĒ”ŗĆĶź³ÉĆ抔Ź±µÄĶŚ¾ņĮ棬ÄĒĆ“¹²ÓŠ¼øÖÖ²»Ķ¬µÄ×āÓĆ·½°ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
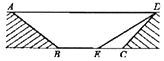
”¾ĢāÄæ”æĪŖ»ŗ½ā½»ĶØÓµ¶Ā£¬Ä³ĒųÄā¼Ę»®ŠŽ½ØŅ»µŲĻĀĶصĄ£¬øĆĶصĄŅ»²æ·ÖµÄ½ŲĆęČēĶ¼ĖłŹ¾(Ķ¼ÖŠµŲĆę ![]() ÓėĶصĄ
ÓėĶصĄ ![]() Ę½ŠŠ)£¬ĶصĄĖ®Ę½æķ¶Č
Ę½ŠŠ)£¬ĶصĄĖ®Ę½æķ¶Č ![]() ĪŖ8Ć×£¬
ĪŖ8Ć×£¬ ![]() £¬ĶصĄŠ±Ćę
£¬ĶصĄŠ±Ćę ![]() µÄ³¤ĪŖ6Ć×£¬ĶصĄŠ±Ćę
µÄ³¤ĪŖ6Ć×£¬ĶصĄŠ±Ćę ![]() µÄĘĀ¶Č
µÄĘĀ¶Č ![]() .
.
£Ø1£©ĒóĶصĄŠ±Ćę ![]() µÄ³¤ĪŖĆ×;
µÄ³¤ĪŖĆ×;
£Ø2£©ĪŖŌö¼ÓŹŠĆńŠŠ×ߵďꏏ¶Č£¬Äā½«Éč¼ĘĶ¼ÖŠµÄĶصĄŠ±Ćę ![]() µÄĘĀ¶Č±ä»ŗ£¬ŠŽøÄŗóµÄĶصĄŠ±Ćę
µÄĘĀ¶Č±ä»ŗ£¬ŠŽøÄŗóµÄĶصĄŠ±Ćę ![]() µÄĘĀ½ĒĪŖ30”ć£¬Ēó“ĖŹ±
µÄĘĀ½ĒĪŖ30”ć£¬Ēó“ĖŹ± ![]() µÄ³¤.(½į¹ū±£ĮōøłŗÅ)
µÄ³¤.(½į¹ū±£ĮōøłŗÅ)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖABŹĒ”ŃOµÄÖ±¾¶£¬ADĒŠ”ŃOÓŚµćA£¬µćCŹĒ ![]() µÄÖŠµć£¬ŌņĻĀĮŠ½įĀŪ£ŗ¢ŁOC”ĪAE£»¢ŚEC£½BC£»¢Ū”ĻDAE£½”ĻABE£»¢ÜAC”ĶOE£¬ĘäÖŠÕżČ·µÄÓŠ( )
µÄÖŠµć£¬ŌņĻĀĮŠ½įĀŪ£ŗ¢ŁOC”ĪAE£»¢ŚEC£½BC£»¢Ū”ĻDAE£½”ĻABE£»¢ÜAC”ĶOE£¬ĘäÖŠÕżČ·µÄÓŠ( )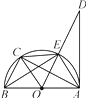
A.1øö
B.2øö
C.3øö
D.4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶź³ÉĻĀĆęµÄÖ¤Ć÷£ŗ
ČēĶ¼£¬ABŗĶCDĻą½»ÓŚµćO£¬EF”ĪAB£¬”ĻC£½”ĻCOA£¬”ĻD£½”ĻBOD£®ĒóÖ¤£ŗ”ĻA£½”ĻF£®

Ö¤Ć÷£ŗ”ß”ĻC£½”ĻCOA£¬”ĻD£½”ĻBOD£¬
Ó֔ߔĻCOA£½”ĻBOD( )£¬
”ą”ĻC£½ ( )£®
”ąAC”ĪBD( )£®
”ą”ĻA£½ ( )£®
”ßEF”ĪAB£¬
”ą”ĻF£½ ( )£®
”ą”ĻA£½”ĻF( )£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖAM”ĪBN£¬”ĻA=60”ć£®µćPŹĒÉäĻßAMÉĻŅ»¶Æµć£ØÓėµćA²»ÖŲŗĻ£©£¬BC”¢BD·Ö±šĘ½·Ö”ĻABPŗĶ”ĻPBN£¬·Ö±š½»ÉäĻßAMÓŚµćC£¬D£®
£Ø1£©Ēó”ĻCBDµÄ¶ČŹż£»
£Ø2£©µ±µćPŌĖ¶ÆŹ±£¬”ĻAPBÓė”ĻADBÖ®¼äµÄŹżĮæ¹ŲĻµŹĒ·ńĖęÖ®·¢Éś±ä»Æ£æČō²»±ä»Æ£¬ĒėŠ“³öĖüĆĒÖ®¼äµÄ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»Čō±ä»Æ£¬ĒėŠ“³ö±ä»Æ¹ęĀÉ£®
£Ø3£©µ±µćPŌĖ¶Æµ½Ź¹”ĻACB=”ĻABDŹ±£¬Ö±½ÓŠ“³ö”ĻABCµÄ¶ČŹż£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬EŹĒAD±ßµÄÖŠµć£¬BE”ĶAC£¬“¹×ćĪŖµćF£¬Į¬½ÓDF£¬·ÖĪöĻĀĮŠĖÄøö½įĀŪ£ŗ
¢Ł”÷AEF”×”÷CAB£»¢ŚCF=2AF£»¢ŪDF=DC£»¢Ütan”ĻCAD= ![]() £®
£®
ĘäÖŠÕżČ·µÄ½įĀŪÓŠ£Ø £©
A.4øö
B.3øö
C.2øö
D.1øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»Ö»µē×Ó¹·“ÓŌµćO³ö·¢£¬°“ĻņÉĻ”śĻņÓŅ”śĻņĻĀ”śĻņĻĀ”śĻņÓŅµÄ·½ĻņŅĄ“Ī²»¶ĻŅĘ¶Æ£¬Ćæ“ĪŅʶÆ1øöµ„Ī»³¤¶Č£¬Ę䊊×ßĀ·ĻßČēĶ¼ĖłŹ¾£¬ŌņA3020µÄ×ų±źĪŖ£Ø £©

A.(1007£¬1)B.(1007£¬©1)C.(504£¬1)D.(504£¬©1)
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com